Binary to decimal conversion is the process of converting a binary number (a number expressed in the base-2 numeral system) into a decimal number (a number expressed in the base-10 numeral system). The binary system uses only two digits, 0 and 1, while the decimal system uses ten digits, from 0 to 9. Understanding how to convert binary to decimal is essential for working with binary data and calculations.
Binary is a base-2 numeral system used in mathematics and computer science. It uses only two symbols, 0 and 1, to represent numbers. Each digit in a binary number represents a power of 2. For example, the binary number “1010” represents (1 * 2^3) + (0 * 2^2) + (1 * 2^1) + (0 * 2^0) = 8 + 0 + 2 + 0 = 10 in decimal.
In computing, binary is fundamental as computers use binary digits (bits) to process and store information. It forms the basis for digital communication, data representation, and computer programming.
Decimal is the base-10 numeral system, the most commonly used system in everyday life. It uses ten symbols (0 to 9) to represent numbers. Each digit in a decimal number represents a power of 10. For example, the decimal number “325” represents (3 * 10^2) + (2 * 10^1) + (5 * 10^0) = 300 + 20 + 5 = 325.
Steps for Binary to Decimal Conversion:
Example:
Convert the binary number 11012 to decimal:
Write down the binary number: 11012
List the powers of 2 from right to left:
23, 22, 21, 20
Multiply each binary digit by the corresponding power of 2:
1 × 23 = 1 × 8 = 8
1 × 22 = 1 × 4 = 4
1 × 21 = 1 × 2 = 0
1 × 20 = 1 × 1 = 1
Sum all the products:
8 + 4 + 0 + 1 = 13
Therefore, the binary number 11012 is equal to the decimal number 1310
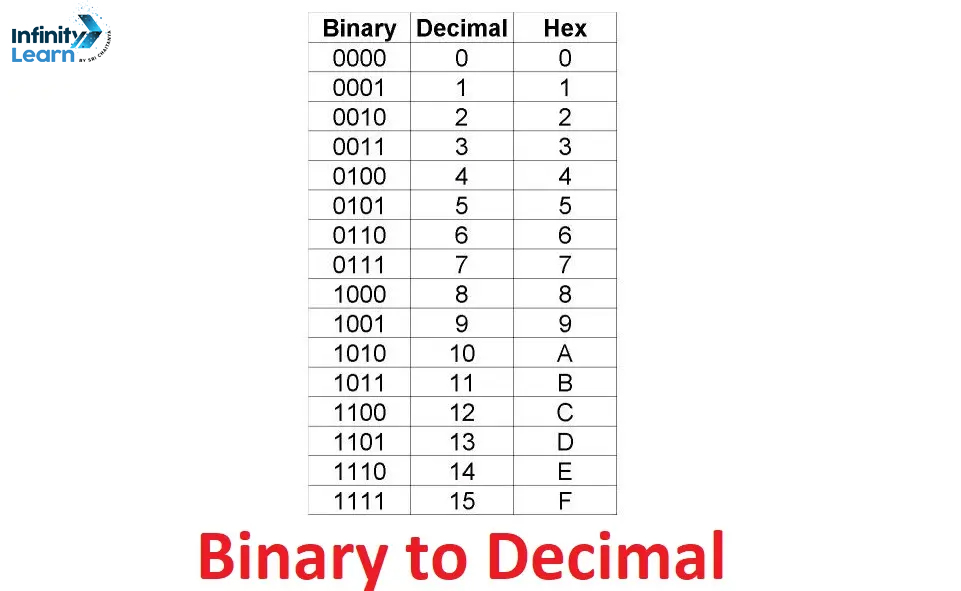
Here is a table containing some binary to decimal converted numbers:
| Binary Number | Decimal Number | Hex Number |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
| 10000 | 16 | 10 |
| 10001 | 17 | 11 |
| 10010 | 18 | 12 |
| 10011 | 19 | 13 |
| 10100 | 20 | 14 |
| 10101 | 21 | 15 |
| 10110 | 22 | 16 |
| 10111 | 23 | 17 |
| 11000 | 24 | 18 |
| 11001 | 25 | 19 |
| 11010 | 26 | 1A |
| 11011 | 27 | 1B |
| 11100 | 28 | 1C |
| 11101 | 29 | 1D |
| 11110 | 30 | 1E |
| 11111 | 31 | 1F |
| 100000 | 32 | 20 |
| 1000000 | 64 | 40 |
| 10000000 | 128 | 80 |
| 100000000 | 256 | 100 |
Here is the Binary to Decimal formula:
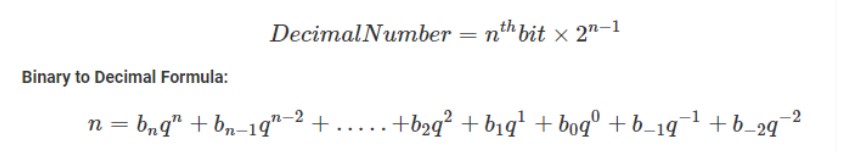
Converting binary to decimal involves multiplying each binary digit by its corresponding power of 2 and then adding up the results. Start from the rightmost digit and move to the left, with the rightmost digit corresponding to 2^0 (1) and each subsequent digit doubling in value (2^1, 2^2, 2^3, and so on).
To convert 10101 binary to decimal: 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 16 + 0 + 4 + 0 + 1 = 21 (decimal)
To convert 1011 binary to decimal: 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 8 + 0 + 2 + 1 = 11 (decimal)
To convert 111010 binary to decimal: 1 * 2^5 + 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0 = 32 + 16 + 8 + 0 + 2 + 0 = 58 (decimal)
To convert 1111 binary to decimal: 1 * 2^3 + 1 * 2^2 + 1 * 2^1 + 1 * 2^0 = 8 + 4 + 2 + 1 = 15 (decimal)
To convert 1100 binary to decimal: 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 0 * 2^0 = 8 + 4 + 0 + 0 = 12 (decimal)