Table of Contents
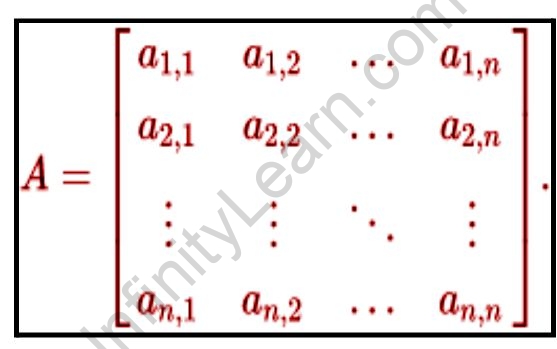
Any rectangular arrangement of numbers in m rows and n columns is called a matrix of order m×n.
Where aij means the component of the ith line and jth section. The above grid is meant as [aij]m×n. The components a11, a22, a33, and so on are called inclining components. Their total is known as the hint of An indicated by Tr(A).
Essential Definitions
(I) Row grid: A lattice having one line is known as a line framework.
(ii) Column lattice: A network having one section is known as a segment framework.
(iii) Square grid: A lattice of request m×n is called a square network if m = n.
(iv) Zero lattice: A = [aij]m×n is known as a zero network, if aij = 0 for all I and j.
(v) Upper three-sided grid: A = [aij]m×n is supposed to be upper three-sided, if aij= 0 for I > j.
(vi) Lower three-sided lattice: A = [aij]m×n is supposed to be lower three-sided, if aij = 0 for I < j.
(vii) Diagonal grid: A square network [aij]m×n is supposed to be inclining, if aij = 0 for I ≠ j.
(viii) Scalar lattice: An inclining network A = [aij]m×n is supposed to be scalar, if aij = k for I = j.
(ix) Unit grid (Identity network): An inclining lattice A = [aij]n is a unit framework, if aij = 1 for I = j.
(x) Comparable frameworks: Two networks An and B are practically identical, assuming they have a similar request.
3. Fairness of frameworks: Two lattices A = [aij]m×n and B = [bij]p×q are supposed to be equivalent, if m = p and n = q and aij = bij ∀ I and j.
4. Multiplication of a matrix by a scalar: Let λ be a scalar, then λA = [bij]m×n where bij= λaij ∀ i and j.
5. Addition of matrices: Let A = [aij]m×n and B = [bij]m×n be two matrices, then A+B = [aij]m×n+ [bij]m×n = [cij]m×n where cij = aij+bij ∀ i and j.
6. Subtraction of matrices: A-B = A+(-B), where -B = ( -1)B.
7. Properties of addition and scalar multiplication:
(i) λ(A+B) = λA+λB
(ii) λA = Aλ
(iii) (λ1+λ2)A = λ1A+λ2A
8. Multiplication of matrices: Let A = [aij]m×p and B = [bij]p×n , then AB = [cij]m×n where cij =
9. Properties of network duplication:
(I) ABBA
(ii) (AB)C = A(BC)
(iii) AIn = A = InA
(iv) For each non-particular square framework A (i.e., | A |≠ 0 ) there exists a remarkable network B with the goal that AB = In = BA. For this situation, we say that An and B are multiplicative inverses of each other. I.e., B = A-1 or A = B-1 .
10. Render of a Matrix.
Let A = [aij]m×n then A’ or AT the render of An is characterized as A’ = [aji]n×m .
(I) (A’)’ = A
(ii) (λA)’ = λA’
(iii) (A+B)’ = A’+B’
(iv) (A-B)’ = A’- B’
(v) (AB)’ = A’B’
(vi) For a square network A, on the off chance that A’ = A, An is supposed to be an asymmetric grid.
(vii) For a square framework A, if A’ = – A, An is supposed to be a slant symmetric network.
11. Submatrix of a lattice:
Allow A to be a given lattice. The grid acquired by erasing a few lines and sections of An is known as a submatrix of A.
12. Properties of determinant:
(I) | A | = | A’ | for any square network A.
(ii) If two lines or two sections are indistinguishable, then, at that point, | A | = 0.
(iii) If | λA | = λn| A |, when A = [aij]n×n.
(iv) If An and B are two square networks of a similar request, then, at that point, | AB |= | A || B |
13. Particular and Non-solitary lattice:
A square grid An is supposed to be solitary, if | A | = 0.
A square lattice An is supposed to be non-particular, if | A | ≠ 0.
14. Cofactor and adjoint framework.
Let A = [aij]n×n be a square network. The framework acquired by supplanting every component of A by the comparing cofactor is known as the cofactor lattice of A. The render of the network of the cofactor of An is known as the adjoint of A, signified as adj A.
15. Properties of adj A.
(I) A . adj A = | A |In = (adj A)A where A = [aij]n×n.
(ii) | adj A | = | A |n-1 , where n is the request for A.
(iii) If A will be an asymmetric network, then, at that point, adj An is additionally symmetric.
(iv) If An is solitary, then, at that point, adj An is additionally particular.
(v) Let A be a nonsolitary framework, then, at that point,
is the multiplicative reverse of An and is meant by A-1.
(vi) (A-1)T = (AT)– 1 for any non particular grid.
(vii) (A-1)– 1 = A, assuming An is non particular.
(viii) A-1 is not particular 100% of the time.
(ix) (adj AT ) = (adj A)T
(x) Let A be a non singular matrix, then AB = AC⇒ B = C and BA = CA ⇒ B = C.
FAQs:
Are matrix and Determinants significant for JEE?
Matrices and Determinants are the vast majority of the least demanding part of selection tests, and yet they assume a significant part in JEE Main and JEE Advanced
Is determinant significant for JEE mains?
Significant Matrices and Determinants Formulas for JEE Main and Advanced. Any rectangular course of action of numbers in m lines and n sections is known as a network of request m×n. Networks and determinants is a significant points for the JEE test. These recipes will assist understudies with having a speedy amendment before the test.

