Addition and Subtraction of Vectors

Introduction

Vectors have each importance and path, one can not absolutely upload two vectors to reap their sum. The addition of vectors is not as honest because of the addition of scalars. To better recognize this, allow us to don’t forget an instance of an automobile travelling 10 miles North and 10 miles South.

Here, the entire distance travelled is 20 miles but the displacement is zero. The North and South displacements are vector quantities, and the alternative instructions cause the individual displacements to cancel each other out. In this text, let us discover ways to carry out the addition and subtraction of vectors.

The study of vectors is important because they are used in many areas of physical science. When vector amounts are included without considering their heading, you’ll get incorrect results.As a matter of physical science, vectors are useful since they address the position, relocation, speed, and speed increases. When drawing vectors, you regularly need more space to attract them to the scale they are addressing, so it is essential to indicate someplace what scale they are being drawn at.

Vector Addition

As already discussed, vectors can’t be actually added algebraically. Following are some factors to consider while including vectors:

• Vectors are brought geometrically and now not algebraically.
• It is necessary to calculate the resultant of vectors that behave independently of each other.
• Vector Addition is nothing however finding the ensuing of a number of vectors performing on a body.

Properties of Vector Addition

Vector addition obeys the following properties.

Vector addition is commutative:–

It approaches that the order of vectors to be delivered collectively does no longer has an effect on the result of the addition. If two vectors are to be added together, then

A+B = B + A

Vector addition is associative:-

While including 3 or more vectors together, the mutual grouping of vectors does not now affect the result.

Mathematically,

a + (b + c ) = (a + b ) + c

Vector addition is distributive:-

In a manner, a scalar times the sum of vectors is identical to the sum of the scalar times of the 2 vectors, in my view.

Mathematically,

ma + mb = m(a + b )

Triangle Law of Vector Addition

The vector addition is accomplished based totally on the Triangle regulation. Let us see what the triangle law of vector addition is:

Assume that we have two vectors:

Now, draw a line AB representing a with A as the tail and B as the head. Draw another line BC (representing b) with B as the tail and C as the head. The line AC is now joined with A at the tail and C at the head. Line AC represents the resultant sum of vectors a and b.

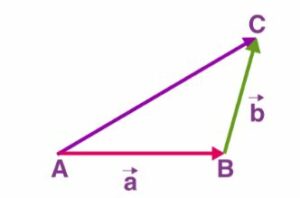
Triangle law of vector addition

The line AC represents a + b

The magnitude of a + b is:

√(a² + b² + 2ab cosθ)

Where,

a= magnitude of vector a,

b= magnitude of vector b,

θ= angle between a and b

The angle with then should be the result of the resultant.

tanΦ= b sinθ/ a+ b cosθ

Let us apprehend this by the manner of an instance. Suppose there are two vectors having identical importance A, and they make a perspective θ with each other. Now, to locate the importance and course of the ensuing, we can use the formulation referred to above.

Let the value of the ensuing vector be B.

B= √(A² + A² + 2AA cos θ)

B = 2 A cos θ/2

Let’s say that the resultant vector makes an angle θ with the first vector then,

tan Φ = A sin θ / A + A cosθ

tan Φ = tan θ/2

Parallelogram law of vector addition

The addition of vectors may also be understood by the law of parallelogram. By the formula, “if two vectors occur simultaneously at one factor and are represented by either side of a parallelogram drawn from it, then their product will be represented by the diagonal line of that parallelogram.”

As indicated by this law on the off chance that two vectors P and Q are addressed by two adjoining sides of a parallelogram both pointing outwards as displayed in the figure underneath, then, at that point, the askew drawn through the convergence of the two vectors addresses the resultant (for example vector amount of Pand Q). Assuming that Q is the relocation from position AD to BC by dislodging it corresponding to itself, this technique becomes comparable to the triangle strategy.

In case of addition of two vectors by parallelogram method as shown in the figure, the magnitude of results will be given by,

(AC)2 = (AE)2 + (EC)2

or R2 = (P + Q cos θ)2 (Q sin θ)2

or R = √(P2+ Q2 )+ 2PQcos θ

The resultant vector P will have the following direction:

tan Φ = CE/AE = Qsinθ/(P+Qcosθ)

Φ = tan-1 [Qsinθ/(P+Qcosθ)]

Vector Subtraction

A vector can be subtracted from another vector by adding them together. Suppose a is to be subtracted from b.

a – b can be said as the addition of the vectors a and (-b). Hence, the formula can be written as follows:

a – b =√(a² + b² – 2ab cosӨ)

–b is nothing but b in the opposite direction.

Also read: General Vectors and Notation

FAQs

1. How do you subtract two vectors?

Ans: Two vectors can be added by law. A triangle is composed of two sides taken in the same order, which represent two vectors (in magnitude and direction), and the third side, taken in the opposite order, represents both vectors (in magnitude and direction).

2. What does triangle law mean?

Ans: The law says that when a body is acted upon by two vectors, each represented by two sides of a triangle, the resultant vector will represent the third side of the triangle.

3. What do you mean by vector subtraction?

Ans: In vector subtraction, a vector difference is calculated, which is the inverse of vector addition.