Table of Contents
Introduction:
In fluid mechanics, Bernoulli’s theorem is the relationship between the pressure, velocity, and height of a moving fluid (liquid or gas), where the compressibility and viscosity (internal friction) are negligible and the flow is either stationary or laminar. First deduced by the Swiss mathematician Daniel Bernoulli (1738), the theorem effectively describes the total mechanical energy of a flowing fluid, including the pressure-related energy of the fluid, the gravitational potential energy of lift, and the kinetic energy. The movement of the fluid remains constant. Bernoulli’s theorem is a principle of conservation of energy in an ideal fluid in a stationary or streamlined flow that underlies many engineering applications.
Overview:
The Bernoulli Principle, formulated by Daniel Bernoulli, states that as the velocity of a moving fluid (liquid or gas) increases, the pressure inside the fluid decreases. Although Bernoulli derived the law, it was Leonhard Euler who derived the Bernoulli equation in its general form in 1752.
Bernoulli’s principle states that the total mechanical energy of a moving fluid, which consists of the gravitational potential energy of elevation, the energy-related to the pressure of the fluid, and the kinetic energy of the fluid’s motion, remains constant.
Bernoulli’s principle can be easily formulated from the principle of conservation of energy.
So, according to Bernoulli’s theorem, if the fluid is flowing horizontally and there is no change in the potential energy of gravity, then a decrease in fluid pressure is related to an increase in fluid velocity.
Bernoulli’s Principle Formula:
Bernoulli’s equation formula is a relationship among pressure, kinetic energy, and gravitational potential energy of a fluid or liquid in a container.
The formula for Bernoulli’s principle will be:
p+½ ρv²+ρg h= constant
Here,
p is the total pressure exerted by the given liquid.
v is the velocity of the given liquid.
is considered the density of the given liquid.
h is the height of the given container.
So, Bernoulli’s equation defines the balance between pressure, velocity and elevation.
Bernoulli’s Equation Derivation:
We have a pipe with varying diameter and height through which an incompressible fluid is flowing. The relationship among the areas of cross-sections A, the flow speed v, height from the ground y, and pressure p at two different points 1 and 2 is given in the figure below.
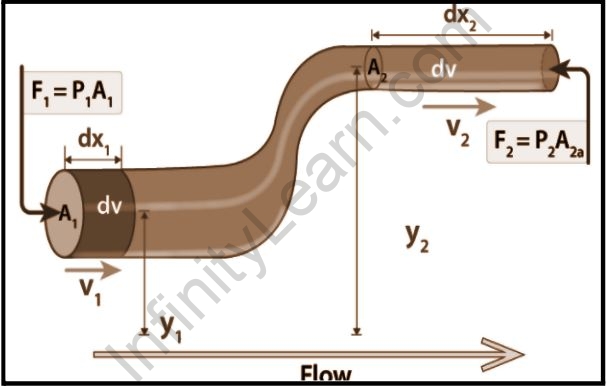
Now, we have two assumptions:
(1) The density of the incompressible liquid stays constant at both points.
(2) The energy of the liquid is conserved as there are no viscous forces in the liquid.
Thus, the total work done on the fluid is given as:
d W=F 1 d x 1-F 2 d x 2
d W=p 1 A 1 d x 1 -p 2 A 2 d x 2
d W=p 1 d V-p 2 d V=(p 1– p 2)d V
It is known that the work done on the liquid was due to the conservation of gravitational force and change in kinetic energy.
Now, the change in kinetic energy of the fluid is given as:
d K=½m 2 v 22 -½ m 1 v 12=½ρd V( v 22-v 12)
Similarly, the change in potential energy is given as:
d U=m g y 2-m g y 1=d V g(y 2-y 1)
Thus, the energy equation is given as:
dW=dK+dU
(P 1-P 2)d V=½ρd(v 1 2 -v 2 2)+ρd V g (y 2-y 1)
P 1–P 2=½v 1 2 –½ v 2 2 +ρ g (y 2–y 1)
Rewriting the above equation, we get
P 1+½v 1 2 +ρ g y 1=P 2+½ v 2 2 +ρ g y 2
This is called Bernoulli’s equation.
Bernoulli’s Equation at Constant Depth
If the liquid moves at a constant depth that is when h1=h2, then Bernoulli’s equation is given as:
P 1+½v 1 2 +ρ g y 1=P 2+½ v 2 2 +ρ g y 2
Bernoulli’s Equation for Static Fluids:
If the fluid is static, then v1=v2=0, then Bernoulli’s equation is given as:
| If v1=v2=0 | P1+ρgh1=P2+ρgh2 |
| If h2=0 | P2=P1+ρgh1 |
Principle of Continuity:
According to the principle of continuity
If fluid flows in a straight line and is incompressible, we can say that the mass of the fluid passing through different sections is the same.

From the above-shown situation, we can conclude that the mass of liquid inside the container remains the same.
Here, we have the rate of mass entering = Rate of mass leaving
The rate of mass entering =ρA 1 V 1 Δt…….(1)
The rate of mass entering =ρA 2 V 2Δt………(2)
Using the above equations, we get
ρA 1 V 1=ρA 2 V 2,
which is known as the Principle of continuity.
Now, we can calculate the speed of efflux for the following setup.
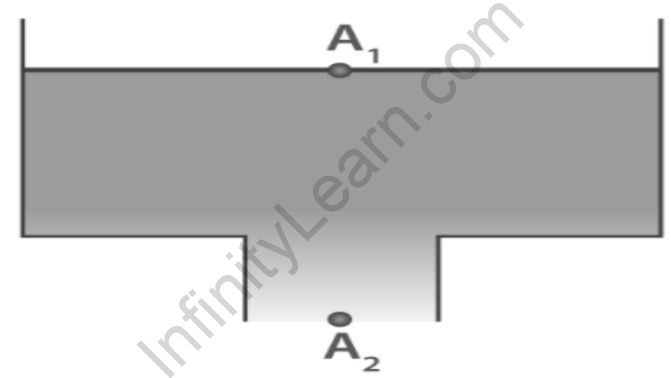
Now, using Bernoulli’s equation at point 1 and point 2,
p+½v 12+ρ g h=p 0+½v 2 2 v 22=v 12+2 p-(p 0/p)+2 g h
In general, A2 is much smaller than A1; in this case, v1 2 is very much smaller than v2 2 and can be neglected.
We then find,
v22=2(p-p0/p)+2gh
When assuming A2<<A1,
We get,
v2=√2gh
Thus,
The velocity of efflux is √2gh.
Uses of Bernoulli Principle:
Bernoulli Principle is used to study unsteady potential flows used in sea level wave theory and acoustics. It is also used to approximate parameters such as fluid pressure and velocity.
Other important Applications of Bernoulli’s Principle are:
(1) Venturi Meter: A device based on Bernoulli’s theorem, used to measure the velocity of a fluid flow through a pipe. Using Bernoulli’s theorem, the Venturi metric formula is given as
V=a 1 a 2 (√2 h g/ a²2-a²2 )
(2) Aircraft operation: The shape of the wing allows air to pass through the top surface at a higher speed than the bottom. The velocity difference is calculated using Bernoulli’s principle to create a pressure difference.
Relationship between Conservation of Energy and Bernoulli’s Equation:
Apply the conservation of energy law to a fluid flow to obtain Bernoulli’s equation. The net work done is the result of changes in fluid kinetic energy and gravitational potential energy. Bernoulli’s equations can be modified depending on the form of energy involved. Other forms of energy include the dissipation of thermal energy due to the viscosity of the fluid.
Also read: Brain Exercises for Better Thinking
Frequently Asked Question (FAQs):
Question 1: What is the meaning of Bernoulli’s equation?
Answer: Bernoulli’s equation is considered as a description of the conservation of energy in a fluid. This is considered a qualitative action to relieve pressure in the high-speed region. This is called the Bernoulli effect.
Question 2: What do you mean by head loss in Bernoulli’s equation?
Answer: The head loss in Bernoulli’s equation is the decrease in total pressure, which is the sum of the velocity head, the head, and the fluid head flowing through the hydraulic system.
Question 3: What is the use of Bernoulli’s Principle?
Answer: Bernoulli Principle is used to study unsteady potential flows used in sea level wave theory and acoustics.







