Table of Contents
Introduction
The De Broglie relation is a physical property of electrons. It was first introduced by the French physicist Louis de Broglie in 1924. The De Broglie relation states that there is a relationship between the wavelength of an electron and its momentum, which is given by p = h/λ where h is the Planck constant and λ is the wavelength. This relation can be used to calculate how much energy an electron has when it collides with another particle, such as a photon. The De Broglie relation is a mathematical equation that relates the momentum of a particle to its wavelength. Using it, we can predict or calculate some properties of particles like their energy levels or their momentum distribution function.
According to the De Broglie relationship, matter, like light, has wave-like and particle-like properties. This nature has been described as dual matter behaviour. De Broglie derived a relationship between matter momentum and wavelength based on his observations. The De Broglie Relationship is the name given to this type of relationship. The De Broglie relation is a mathematical equation that describes the probability of a particle having a particular wavelength. It is used in quantum mechanics and quantum physics to explain how particles can have different wavelengths. The De Broglie relation is named after the French physicist, Louis de Broglie, who first described it in 1924.
Overview
The de Broglie relation is a mathematical relation between the wave function of a particle and the wave function of its antiparticle. The de Broglie relation is a mathematical relation between the wave function of a particle and the wave function of its antiparticle. It was proposed by French physicist Louis-Victor de Broglie in 1924 and is named after him. De Broglie’s idea was that they are related by an equation, but it was not until 1957 that physicists David Bohm, Eugene Wigner, and John von Neumann found that quantum mechanics can be described in terms of probability waves. Bohr’s model did not explain many concepts related to the spectrum of various atoms and the splitting of spectral lines in magnetic and electric fields. To address the shortcomings of Bohr’s atomic model, efforts were made to develop a more comprehensive atomic model.
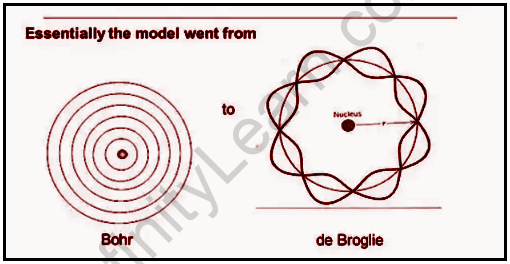
This is a model that explains the behavior of electrons in atoms. It was developed by Louis de Broglie in 1924. This model helps us understand how waves and particles can be described as one entity at the same time. This is also known as wave-particle duality. In this model, electrons are represented as waves, and protons are represented as particles. The de Broglie relation provides a formula for calculating the wavelength for an electron moving through space and time according to its momentum or speed. The de Broglie relation states that the wavelength of a photon is equal to the frequency of light. This means that light has both a wave and particle nature. The de Broglie relation can be used to measure how much momentum an electron has by measuring how much momentum it takes for an electron to change its wavelength. This equation makes it possible to calculate what wavelength an electron would have if it had more or less energy than its actual value.
Relation between de broglie wavelength and kinetic energy
There is a relation between de Broglie wavelength and kinetic energy. De Broglie wavelength is the distance traveled by a particle during its time of flight, while kinetic energy is the force that moves the particle. When particles are moving in a straight line, there is a constant velocity for them and their de Broglie wavelength will be equal to their velocity. When particles are moving at an angle to the straight line, their de Broglie wavelength will be smaller than their velocity. The shorter the de Broglie wavelength, the greater the kinetic energy because there is less distance that has to be traveled for it to reach its maximum speed. A de Broglie wavelength is the distance that a particle travels in its orbit, and it is proportional to the momentum of the particle. A derivation of kinetic energy from de Broglie wavelength can be found here: E=hv
Kinetic energy is initially provided by:
E=½mv²
=p²/2m
p=√2mE
where m is the particle’s mass, v is its speed, and p is its momentum
The wavelength of De-Broglie is given by,
λ=h/p
λ=h/√2mE
Derive de broglie relationship
One of the developments that had a significant impact on the formulation was the investigation of the dual behaviour of matter. Given the particle nature, Einstein’s equation is as follows:
E=mc²..……(1)
Where,
E stands for energy.
m stands for mass.
c = light speed
Given the wave nature, the Plank’s equation is as follows:
E=hv……(2)
Where,
E stands for energy.
Plank’s constant = h
v stands for frequency.
(1) and (2),
mc²=hv……….(3)
The frequency, v, can be expressed in terms of wavelength, as follows:
v=c/λ
For a general particle, c can be replaced by the object’s velocity, v. As a result, equation (3) can be written as follows:
mv2=hv/λ
=h/mv
The above equation is referred to as the de Broglie relationship, and the wavelength is referred to as the de Broglie wavelength.
Relation between wavelength and momentum
In the case of a light wave, the momentum of the wave is inversely proportional to its wavelength. This relationship is called the de Broglie relation and it can be explained with a simple thought experiment. Imagine two electrons traveling at different velocities and positions. If they were to collide, they would impart momentum to each other. This can be represented by giving them different wavelengths, which are then related by momentum and wavelength:
P = mv
The distance between two successive crests or troughs of a wave is commonly defined as its wavelength. Because it is measured in the direction of the wave, it produces an inverse relationship between wavelength and frequency. As a result, the wavelength formula is represented as,
λ=v/f
The wavelength is also known as the De Broglie wavelength in this context.
It is defined as a property of a moving body that is measured using its mass and the velocity at which the body is moving. As we all know, momentum refers to a body that has both mass and motion. As a result, the momentum formula is represented as
M=mv
The following is the relationship between wavelength and momentum. As we all know, wavelength and momentum are inversely proportional to one another.
λ∝1/M
By replacing the proportionality sign with equal to, we obtain the proportionality constant,
λ=k/M
In this case, k = h = Planck’s Constant.
We can now write the above equation as,
λ=h/M
There is a relationship between a moving particle’s wavelength and momentum.
FAQs
What exactly is the relationship between kinetic energy and wavelength?
Because velocity equals frequency × wavelength. As a result, kinetic energy is proportional to (wavelength) 2 or the square of the wavelength.
What is de Broglie's significance?
Wave-like properties can be found in all particles. A particle's de Broglie wavelength indicates the length scale at which wave-like properties are important to that particle.





