Table of Contents
Introduction to Kepler’s Laws
The concept of motion is always relative. There are two types of motions based on the energy of the particle in motion:
- Bounded Motion
- Unbounded Motion
The particle has negative total energy (E<0) inbounded motion and has two or more extreme points where the total energy is always equal to the potential energy, i.e. the kinetic energy of the particle is zero.
E< 0 implies bounded motion for eccentricity 0 ≤ e <1. Circular orbits have eccentricity e = 0, and elliptical orbits have eccentricity e < 1.
In unbounded motion, the particle has positive total energy (E > 0) and has a single extreme point where the total energy is equal to the potential energy of the particle, thus the kinetic energy of the particle becomes zero.
E > 0 implies unbounded motion for eccentricity e= 1. The eccentricity of a parabolic orbit is 1, while the eccentricity of a hyperbolic path is greater than 1.
Kepler’s Laws of Motion:
The Law of Orbits – Kepler’s First Law:
As per Kepler’s initial law,” All the planets whirl the sun in curvilinear circles having the sun at one in all the foci”. The place where the world is close to the sun is thought of as a point of periapsis and also the place where the world is farther from the sun is thought of as apoapsis.
It is the attributes of a circle that the number of the distances of any planet from 2 foci is steady. The circular circle of a planet is in command of the event of seasons.
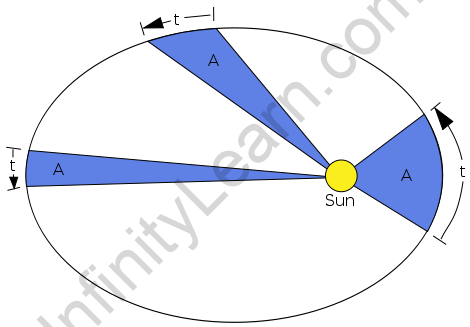
The Law of Equal Areas – Kepler’s Second Law
According to Kepler’s resulting law, “the vary vector attracted from the sun to the world clears out equivalent regions in equivalent times.”
The planet’s kinetic energy is not constant in its path because its orbit is not circular. Having more kinetic energy near the perihelion and less kinetic energy near the aphelion implies that it is traveling faster (v min ) at the perihelion and slower (v max ) at the aphelion. When r is the distance between the planet and the sun at perihelion (r min ) and aphelion (r max ), then,
rmin + rmax = 2a × (length of major axis of an ellipse) . . . . . . . (1)
Now consider a small area ΔA described in a small time interval Δt and the covered angle is Δθ. Let the radius of curvature of the path be r, then the length of the arc covered = r Δθ.
ΔA = 1 /2[r.(r.Δθ)]= 1 / 2 r2 Δθ
Therefore,
ΔA/Δt = [ 1 / 2 r 2]Δθ/dt
limΔt→0 ΔA /Δt = 1 / 2 r 2 Δθ/Δt taking limits both side as, Δt→0
dA / dt = 1 / 2 r2 ω
dA / dt = L / 2m
Thus,
dA/dt = constant
The area swept back in an equal interval of your time could be a constant.
Kepler’s resulting law will likewise be expressed as “The region speed of a planet rotating around the sun within the curvilinear circle stays steady that infers the precise force of a planet stays consistent”. Because the rakish energy is steady, all planetary movements square measure plate like movements, which is a direct result of focal power.
The Law of Periods – Kepler’s Third Law
Following the law of periods, the sq. of the period of the associate upset of a planet around the sun in a very circular circle corresponds to the 3D form of its semi-significant pivot”.
T 2 ∝ a 3
More restricted the circle of the world around the sun, additional restricted the time taken to end one upheaval. Utilizing the conditions of the law of motion of enticing energy and laws of movement, Kepler’s third law takes an additional broad structure:
P2 = 4π2 /[G(M1+ M2)] × a3
Kepler’s Third Law treats and analyzes the orbital amount and sweep of a planet’s circle in relevancy to those of alternative planets. In opposition to Kepler’s initial and second laws, which describe the movement characteristics of one planet, the stargazer’s third law examines the movement of multiple planets and determines the harmonies between them.
This comparison takes the shape of the quantitative relation between the squares of the periods (T2) and their average distances from the sun (R3), finding that it’s equivalent for every planet.
Also read: Here’s How to Boost Your Percentage in the Board
Frequently Asked Questions:
Question 1: Why are Kepler’s 1st and 2nd laws important?
Answer: Kepler’s initial 2 laws were vital for a variety of reasons. They created a sense of the universe’s structure – astronomers might finally throw out the epicycles and also the equant and construct a simplified version of the Copernican universe.
Question 2: Did Pluto meet the standard of planetary motion according to Kepler?
Answer: Yes! All objects in orbit follow Kepler’s Second Law and every one of Kepler’s alternative laws too. Like several alternative objects in our system, Pluto moves quickly once it’s nearer to the sun and slower once it’s farther away.
Question 3: What are the applications of Kepler’s law and how is it relevant to modern astronomy?
Answer: Kepler’s laws describe the orbit of planets (and asteroids, comets, and cometoids) around the sun. They’ll even be accustomed to describing how moons orbit around a planet. But, they do not simply apply to our system — they’ll be accustomed to describing the orbits of associate exoplanets around any star.
Question 4:What is the use of Kepler’s second law?
Answer: The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law helps to establish that when a planet is closer to the Sun, it travels faster. Stargazer himself never numbered these laws or notably recognized them from his completely different disclosures.





