Table of Contents
Introduction
Multiplication comes after addition and subtraction in the development of simple arithmetic. In vector analysis, multiplication is the multiplication of a vector by a scalar, which corresponds to scalar multiplication. A+A is expressed as 2A, and A+ A+…n terms = n A, where n is a scalar value. In vector analysis, there is another sort of multiplication that involves the product of two vector values. Vector products are introduced because they are frequently encountered in the investigation of physical problems.
There are two ways for multiplying two vectors, both of which have been shown to be extremely useful while solving numericals. We know these two methods as the Scalar product and Vector Product.
Without a question, mathematics is the language of physics. When one has a good understanding of mathematics, it is easier to articulate, interpret, and apply physical principles. We’ll also use algebra, trigonometry, geometry, vector algebra, differential calculus, and integral calculus on a frequent basis. This course will discuss vectors, vector equality, unit vectors, and position vectors. Using simple algebraic concepts, certain physical quantities can be completely described mathematically (with units provided) and added. And even if you’re just a science student, you’ll need to understand vectors. It’s almost as though you can’t think of mechanics without them. For conceptual clarity, the principles are essential. Continue to explore our page for more physics-related information.
Product of two vectors as a scalar or as a dot product or as an inner product
Using two vectors as inputs, we can create a scalar product
AB=ABcos?

When two vectors are positioned tail to tail, the scalar product is equal to the product of their magnitudes and the cosine of the smaller angle between them.
Geometrical Interpretation of Scalar Product
We can write AB=ABcos? as AB=B(Acos?)
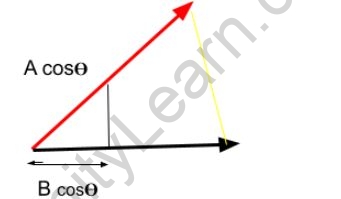
Thus we can conclude that AB=ABcos?
= A measure of the magnitude of the component of the in the direction of A
=ABA
Properties of Dot Product
It follows commutative property
ab=ba
AB=ABcos?
AB=BAcos?
It follows distributive property
a.(b + c) = a.b + a.c
It follows Bilinear Property
a.(rb + c) = r.(a.b) + (a.c)
Scalar Multiplication Property
(xa) . (yb) = xy (a.b)
As the dot product of a scalar and a vector is forbidden, it follows the Non-Associative property.
Unit vectors in the directions of the x, y, and z axes are i, j, and k, respectively
If i × j = 0, then i × k = 0, and j × k = 0, then
One is equal to j × j, one is equal to k × k, one is equal to one
If a=a1i+a2j+a3k and b=b1i+b2j+b3k
ab=a1b1+a2b2+a3b3
Note: An interesting way to remember this is to multiply the I and j components together, then multiply the k and k components together, and lastly sum the results. This form is occasionally referred to as the inner product of vectors a and b. This simply means the sum of the products of the respective vector components in the context of vectors.
Applications of Scalar Product
Using two vectors, find the angle between them
When two vectors are written in cartesian form, one of the most typical applications of the scalar product is to compute the angle between them.
From the scalar product’s definition,
a · b = |a| |b| cos θ
By rearrangement, we can get the following expression for cos θ:
cos θ =a · b/|a| |b|
Force and displacement together determine the work done by a constant force.
Vector Multiplication
Geometrically, the area of the parallelogram formed by two vectors is called the cross product or Vector Multiplication/product.
The name “cross product” comes from the symbol used to symbolize this operation, which is a huge diagonal cross (). This product is also known as the vector product because it contains magnitude and direction.
AB=ABsin?n
A unit vector perpendicular to the plane produced by the two vectors is n (n hat). The right-hand rule determines the direction of n.
The cross product is distributive
This is defined as (A ×B + C) = (A × B + C)
but not commutative
A × B = −B × A
It’s worth noting that the magnitude of the cross product of any unit vector with any other is one. (After all, the sine of 90° is one.) However, the orientation is not immediately apparent. Using the right-hand rule for cross-multiplication we can determine the direction of the two vectors as well as their product. It is extremely crucial to order the operations correctly because cross multiplication is not commutative.
- Hold your right-hand flat and perpendicular to your fingers, with your thumb perpendicular to your fingers. At no time should you bend your thumb.
- Point your fingers in the first vector’s direction.
- Orient your palm such that your fingers point in the direction of the second vector when you fold them.
- The cross product now has your thumb pointing in the right way.
Any cyclic product of the three coordinate axes is positive, whereas any anti-cyclic product is negative in a right-handed coordinate system, which is the most common coordinate system used in physics and mathematics. Consider a clock that displays the three letters x-y-z instead of the traditional twelve numerals. A cyclic and positive product of these three letters is one that runs around the clock in the same direction as the sequence x-y-z. Anti Cyclic and negative products are those that run in the opposite direction.
Also read: Addition and Subtraction of Vectors
Frequently Asked Questions
Question 1: How Do You Calculate Vector Scalar Multiplication?
Answer: In three simple steps, scalar multiplication of vectors may be determined. To begin, calculate the magnitude of the two vectors a and b, i.e. |a| and |b|. Next, calculate the cosecant of the angle formed by the two vectors. To get the dot product of the two vectors, multiply the magnitude of the two vectors by the and cosecant of the angle between the two vectors. AB=ABcos?
Question 2: Why is the Scalar Multiplication of Vectors called the Dot Product?
Answer: Because all of the components of the solution are scalar values, the dot product is called scalar multiplication of vectors.
Question 3: What is the definition of vector multiplication?
Answer: When two vectors are multiplied together, the outcome is a third vector that is perpendicular to the two original vectors. The area of the parallelogram between them determines the magnitude of the resultant vector, and the right-hand thumb rule determines its direction. a b = c, where c is the cross product of the two vectors a and b, or vector multiplication.





