Table of Contents
Introduction:
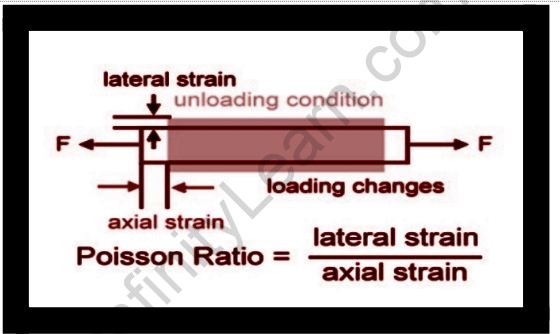
Poisson’s ratio is the inverse of the ratio of transverse strain to lateral or axial strain in mechanics. It is also the ratio of the total transversal expansion to the amount of axial compression for low values of these changes, and it is named after Simeon Poisson and symbolized by the Greek letter ‘nu’.
“The proportion of transverse contractions strain to longitudinal extension strain in the site of the stretching force,” as defined by Poisson. Here,
- Compressive deformation is regarded as a bad thing.
- Tensile deformation is regarded as a good thing.
Poisson’s ratio formula =Transverse strain/ Longitudinal strain
⇒ ν=−εt/εl
where,
The Lateral or Transverse Strain is what it’s called εt
The Longitudinal or Axial Strain is denoted by the letter εl
The Poisson’s Ratio is symbolized by v
The change in dimension (length, breadth, area, etc.) divided by the original dimension is the strain.
A brief outline:
Effect of Poisson:
When a material is extended in one direction, it compresses in the opposite direction, and vice versa. The Poisson’s ratio is to measure the magnitude of this occurrence. When a rubber band is stretched, for example, it tends to get thinner.
Values of Poisson’s ratio for various materials:
In the direction of the stretching force, it is the ratio of transverse contraction strain to longitudinal extension strain. With the application of force on a body, stress and strain relationships can be formed.
- Poisson’s ratio is positive for tensile deformation.
- It is negative for compressive deformation.
Although the longitudinal strain is positive, the negative Poisson ratio indicates that the material will exhibit positive strain in the transverse direction. Poisson’s ratio is usually in the range of 0 to 0.5 for most materials.
Simply explained, Poisson’s ratio is a measurement of how much a material’s width or diameter changes when it is dragged lengthwise. It is the ratio of the change in lateral (transverse) strain to the change in linear (axial) strain, in more technical language. Pulling a rubber band is the most basic example of this. The rubber band’s width narrows dramatically as it is stretched in one direction. That indicates a high Poisson’s ratio.
Important concepts:
Poisson’s ratio is a unit less number since it is a statistic of one strain divided by another. Poisson’s ratios of very flexible, low-modulus materials, such as rubber, can be as high as 0.5, whereas Poisson’s ratios of very rigid, high-modulus materials, such as concrete, are often very close to 0. However, some materials have Poisson’s ratios as low as -1, implying that when they are dragged lengthwise, the material’s width or diameter will rise. A Hoberman sphere, which can be obtained at any toy store, is the most relatable instance of this.
Some Points to Consider Regarding Poisson’s Ratio Value
- The value of Poisson’s ratio is both a scalar and a dimensionless unitless number.
- It has a positive value for tensile deformation and a negative value for compressive deformation.
- There would be no change in the diameter or width of an object when Poisson’s Ratio approaches zero (0).
For material, the Poisson’s Ratio is defined as:
The Poisson’s Ratio is the ratio of a material’s transverse contraction to its longitudinal extension strain in the direction of the stretching force. The stress or strain might be created by the body exerting force on the material. For compressive deformation, the Poisson’s ratio is negative, but for tensile deformation, the Poisson’s ratio is positive. The positive strain is in the transverse direction, according to the negative Poisson’s ratio. For the most part, Poisson’s Ratio is in the range of 0 to 0.5.
Poisson’s Ratio is usually significant since most common materials get narrower in the opposing or cross direction when extended. Most materials resist changes in volume, as defined by the bulk modulus K also known as B, more than changes in shape, as determined by the shear modulus G. The shape distortion also causes the interatomic connections to realign.
Bending Poisson’s Ratio:
The Poisson’s Ratio governs the curvature of a bar or plate in the direction perpendicular to the bending. In the circumstance of bending a rubber, the anticlastic curvature is plainly visible.
Anisotropy and Poisson’s Ratio:
The physical properties of anisotropic solids, such as honeycombs, single crystals, and various fibrous composites, are affected by the direction in which they are stretched or bent, including the Poisson’s ratio and Elastic Moduli. Because of the huge magnitude of this type of anisotropic material, Poisson’s ratio might be positive or negative.
Significance of Poisson’s ratio in NEET exam:
The entire world has changed to an online method of schooling in the post-pandemic age. It’s critical at this moment to select the correct educator so that you can receive a high-quality education while sitting at home. Infinity Learn has a number of advantages over the competitors, including:
Experts and experienced instructors in the subject provide answers. The answers are in accordance with CBSE and NCERT criteria for the NEET test, assisting students in achieving higher results. The courses are reasonably priced, and there are some free courses available for new students to test out. On the same platform, there is a diverse choice of courses ranging from kindergarten to twelfth grade, as well as particular programs for competitive exams such as NEET.
Also read: Young’s Modulus
FAQ (Frequently asked questions):
Question 1: Is Poisson’s Ratio Constant?
Answer: Within elastic limits, Poisson’s ratio for material remains nearly constant.
Question 2: What is Poisson’s ratio?
Answer: In the orientation of the displacements, the ratio of transverse strain to longitudinal strain.
Question 3: What are the units of Poisson’s ratio?
Answer: The unit less scalar quantity is Poisson’s ratio.
Question 4: What are some possible applications of the Poisson effect in the real world?
Answer: These are some examples of how the Poisson effects are used in the real world.
Using “Cork” as a bottle stopper: Due to its extremely low Poisson ratio, cork is the most suited material for use as a bottle stopper. This means that even when heavy compression is applied on both sides of the cork, the cork does not change much. When rubber is employed as a bottle stopper, however, it will stretch laterally if subjected to axial compression, causing the stopper to become trapped in the bottle.







