Table of Contents
- Decimal Representation of Rational Numbers
- Summary
- What’s Next?
In the previous segment, we saw Different Categories of Numbers that come under Real Numbers. In this segment let us see the Decimal Representation of Rational Numbers.
What is the Decimal representation of rational numbers?
A rational number is a number that can be expressed as ?, where ? ≠ 0
?
There are different types in which a rational number can be written in a decimal form.
There are two broad categories: Terminating decimals and Non-Terminating decimals. Non-Terminating is again classified into two types: Recurring decimals and Non-Recurring decimals.
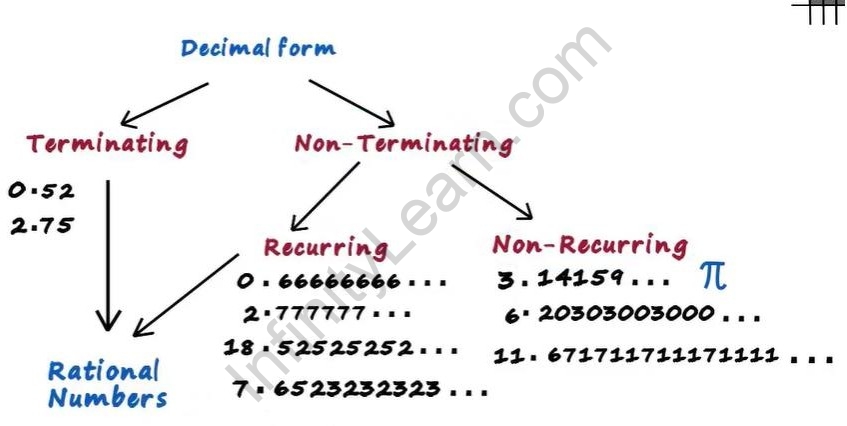
Decimal Forms
Terminating decimals and non-terminating recurring decimals together form rational numbers.
Non-terminating non-recurring decimals cannot be expressed as \[ \frac{p}{q} \] and hence, they are not rational numbers.
Summary
| Rational Numbers |
|

