Table of Contents
For the advantage of students studying for the CBSE Term II Class 10 Maths test, NCERT Exemplar Solutions for Class 10 Maths Chapter 5 Arithmetic Progression are offered here. Students must become familiar with these NCERT Exemplar Solutions to achieve a good grade in the Class 10 examination. The specialists at Infinity Learn answer these NCERT difficulties. These answers will assist you in comprehending and mastering various types of arithmetic progressions questions. NCERT Exemplar Solutions assist you in achieving proficiency in solving all types of queries.
NCERT Exemplar Class 10 Maths Chapter 5 Exercise 5.1
Choose the correct answers from the given four options:
Question 1.
In an AP, if d = -4, n = 7, an = 4, then a is equal to
(A) 6
(B) 7
(C) 20
(D) 28
Solution:
(D)
In an AP,
an = a + (n – 1 )d
⇒ 4 = a + (7 – 1) (-4) [by given conditions]
⇒ 4 = a + 6(-4) ⇒ 4 + 24 = a
∴ a = 28
Question 2.
In an AP, if a = 3.5, d = 0,n = 101, then an will be
(A) 0
(B) 3.5
(C) 103.5
(D) 104.5
Solution:
(B)
In an AP,
an = a + (n – 1)d = 3.5 + (101 – 1) × 0
[by given conditions]
∴. an = 3.5
Question 3.
The list of numbers – 10, – 6, – 2, 2,… is
(A) an AP with d = -16
(B) anAP with d = 4
(C) an AP with d = – 4
(D) not an AP
Solution:
(B)
The given numbers are -10, -6, -2, 2,
Here, a1 = -10, a2 = -6, a3 = 2 and a4 = 2,….
Since a2 – a1 = -6 – (-10) = -6 + 10 = 4
a3 – a2 = -2 – (-6) = -2 + 6 = 4
a4 – a3 = 2-(-2) = 2 + 2 = 4
………….
…………
………….
Each successive term of given list has same difference i.e., 4
So, the given list forms an AP with common difference, d = 4
Question 4.
The 11th term of the AP: -5, −52 , 0, 52,…
(A) -20
(B) 20
(C) -30
(D) 30
Solution:
(B)
Given AP -5, −52 , 0, 52,…
Here, a = -5, d = −52+5=52
∴ an = a + (11 – l)d [∵ an = a + (n – 1)d]
= -5 + (10) × 52
= -5 + 25 = 20
Question 5.
The first four terms of an AP, whose first term is -2 and the common difference is -2, are
(A) -2, 0, 2, 4
(B) -2, 4, -8, 16
(C) -2, -4, -6, -8
(D) -2, -4, -8, -16
Solution:
(C)
Let the first four terms of an AP are
a, a + d, a + 2d and a + 3d
Given, that first term, a = -2 and common
difference, d = -2, then we have an AP as follows
-2, -2 -2, -2 + 2(-2), -2 + 3(-2)
= -2, -4, -6, -8
Question 6.
The 21st term of the AP whose first two terms are -3 and 4 is
(A) 17
(B) 137
(C) 143
(D) -143
Solution:
(B)
Given, first two terms of an AP are a = -3 and a + d = 4
⇒ — 3 + d = 4
Common difference, d = 7
⇒ a21 = a + (21 – 1)d [∵ an = a + (n – 1)d]
= -3 +(20)7
= -3 + 140 = 137
Question 7.
If the 2nd term ofanAPis13and the 5th term is 25, what is its 7th term?
(A) 30
(B) 33
(C) 37
(D) 38
Solution:
(B)
Given a2 = 13 and a5 = 25
⇒ a + (2 – 1)d = 13 [∵ an = a + (n – 1)d]
and a + (5 – 1 )d = 25
⇒ a + d = 13 ……….. (i)
and a + 4d = 25 ………… (ii)
On subtracting Eq. (i) from Eq. (ii), we get
3d = 25 – 13 = 12
⇒ d = 4
From Eq. (i) a = 13 – 4 = 9
∴ a7 = a + (7 – 1)d = 9 + 6 × 4 = 33
Question 8.
Which term of the AP: 21, 42, 63, 84,… is 210?
(A) 9th
(B) 10th
(C) 11th
(D) 12th
Solution:
(B)
Let nth term of the given AP be 210.
Here, first term, a = 21
and common difference, d = 42 – 21 = 21 and an = 210
∵ an = a + (n – 1 )d
⇒ 210 = 21 + (n- 1)21
⇒ 210 = 21 + 21n- 21
⇒ 210 = 21n ⇒ n = 10
Hence, the 10th term of an AP is 210.
Question 9.
If the common difference of an AP is 5, then what is a18 – a13?
(A) 5
(B) 20
(C) 25
(D) 30
Solution:
(C)
Given, the common difference of AP i.e., d = 5
Now, a18 – a13 = a + (18 – 1)d – [a + (13 – 1)d]
[∵ an = a + (n – 1)d] = a + (17 × 5) – a – (12 × 5)
= 85 – 60 = 25
Question 10.
What is the common difference of an AP in which a18 – a14 = 32?
(A) 8
(B) -8
(C) -4
(D) 4
Solution
(A)
Given, a18 – a14 = 32
⇒ a + (18 – 1)d – [a + (14 – 1)d] = 32
[∵an = a + (n – 1 )d]
⇒ a + 17d – a – 13d = 32
⇒ 4d = 32
∴ d = 8
which is the required common difference of an AP.
Question 11.
Two APs have the same common difference. The first term of one of these is -1 and that of the other is – 8. Then the difference between their 4th terms is
(A) -1
(B) -8
(C) 7
(D) -9
Solution:
(C)
Let the common difference of two APs are d1 and d2, respectively.
By given condition, d1 = d2 = d ……….. (i)
Let the first term of first AP(a1) = -1
and the first term of second AP (a2) = -8
We know that, the nth term of an AP
Tn = a + (n – 1)d
∴ 4th term of first AP,
T4 = a1 + (4 – 1)d = -1 + 3d
and 4th term of second AP,
T4‘ = a2 + (4 – 1)d = -8 + 3d
Now, the difference between their 4th terms is i.e.,
∣∣T4−T′4∣∣ = (-1 + 3d) – (-8 + 3d)
= -1 + 3d + 8 – 3d = 7
Hence, the required difference is 7.
Question 12.
If 7 times the 7th term of an AP is equal to 11 times its 11th term, then its 18th term will be
(A) 7
(B) 11
(C) 18
(D) 0
Solution:
(D)
According to the question,
7a7 = 11a11
⇒ 7[a + (7 – 1)d] = 11 [d + (11 – 1)d]
[∵ an = a + (n – 1 )d]
⇒ 7(o + 6d = 11 (a + 10d)
⇒ 7a + 42d = 11a + 10d
⇒ 4a + 68d = 0
⇒ 2(2a + 34d) = 0
⇒ 2a + 34d = 0
⇒ a + 17d = 0 …………. (i)
∴ 18th term of an AP, a18 = a + (18 – 1)d = a + 17d = 0
[from Eq(i)]
Question 13.
The 4th term from the end of the AP: -11, -8, -5, 49 is
(A) 37
(B) 40
(C) 43
(D) 58
Solution:
(B)
We know that, the nth term of an AP from the end is
an = l -(n – 1 )d …………. (i)
Here, l = Last term = 49 [given]
Common difference, d = -8 – (-11) = -8 + 11 = 3
From Eq (i), a4 = 49 – (4 – 1) 3 = 49 – 9 = 40
Question 14.
The famous mathematician associated with finding the sum of the first 100 natural numbers is
(A) Pythagoras
(B) Newton
(C) Gauss
(D) Euclid
Solution:
(C)
Gauss is the famous mathematician associated with finding the sum of the first 100 natural numbers i.e., 1, 2, 3,100.
Question 15.
If the first term of an AP is -5 and the common difference is 2, then the sum of the first 6 terms is
(A) 0
(B) 5
(C) 6
(D) 15
Solution:
(A)
Given, a = -5 and d = 2
∴ S6 = 62 [2a + (6 – 1)d] [∵ Sn = n2 [2a + (n – 1)d]
= 3[2(-5) + 5(2)] = 3(-10 + 10) = 0
Question 16.
The sum of first 16 terms of the AP: 10, 6 2, … is
(A) -320
(B) 320
(C) -352
(D) -400
Solution:
(A)
Given, AP is 10, 6, 2,
Here, first term a = 10, common difference, d = – 4
∴ S16 = 162 [2a + (16 – 1)d]
[∵ Sn = n2 [2a + (n – 1)d]
= 8[2 × 10 + 15(-4)]
= 8(20 – 60) = 8(-40) = -320
Question 17.
In an AP if a = 1, a„ = 20 and Sn = 399, then n is
(A) 19
(B) 21
(C) 38
(D) 42
Solution:
(C)
[∵ Sn = n2 [2a + (n – 1)d]
399 = n2 [2 × 1 + (n – 1)d] [∵ a = 1]
798 = 2n + n(n – 1)d ………… (i)
and, an = 20
⇒ a + (n-l)d = 20 [∵ an = a + (n – 1)d]
⇒ 1 + (n – 1)d = 20⇒ (n – 1d = 19 ……… (ii)
Using Eq. (ii) in Eq. (i), we get
798 = 2n + 19 n
⇒ 798 = 21n
∴ n = 79821
Question 18.
The sum of first five multiples of 3 is
(A) 45
(B) 55
(C) 65
(D) 75
Solution:
(A)
The first five multiples of 3 are 3, 6, 9,12 and 15.
Here, first term, a = 3, common difference, d = 6 – 3 = 3 and number of terms n = 5
∴ S5 = 52 [2a + (5 – 1)d]
[∵ Sn = n2 [2a + (n – 1)d]
= 52 [2 × 3 + 4 × 3] = 52 (6 + 12) = 5 × 9 = 45
NCERT Exemplar Class 10 Maths Chapter 5 Exercise – 5.2
Question 1.
Which of the following form an AP? Justify your answer.
(i) -1,-1,-1,-1,…
(ii) 0,2,0,2,…
(iii) 1,1,2,2,3,3,…
(iv) 11,22,33,…
(v) 12,13,14,….
(vi) 2,22, 23, 24, …
(vii) 3–√,12−−√,27−−√,48−−√,…
Solution:
(i) Here, t1 = -1, t2 = -1, t3 = -1 and t2 = -1
t2 – t1 = -1 + 1 = 0
t3 – t2 = —1 + 1 = 0
t4 – t3 = -1 + 1 = 0
Clearly, the difference of successive terms is same, therefore given list of numbers form an AP.
(ii) Here, t1 = 0, t2 = 2, t3 = 0 and t4 = 2
t2 – t1 = 2 – 0 = 2
t3 – t2 = 0 – 2 = -2
t4 – t3 = 2 – 0 = 2
Clearly, the difference of successive terms is not same, therefore given list of numbers does not form an AP.
(iii) Here, t1 = 1, t2 = 1, t3 = 2 and t4 = 2
t2 – t1 = 1 -1 = 0
t3 – t2 = 2 – 1 = 1
t4 – t3 = 2 – 2 = 0
Clearly, the difference of successive terms is not same, therefore given list of numbers does not form an AP.
(iv) Here, t1= 11, t2 = 22 and t3 = 33
t2 – t1 = 22 – 11 = 11
t3 – t2 = 33 – 22 = 11
Clearly, the difference of successive terms is same, therefore given list of numbers form an AP.
(v)
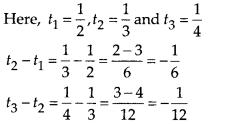
Clearly, the difference of successive terms is not same, therefore given list of numbers does not form an AP.
(vi) 2, 22, 23, 24,… i.e., 2, 4, 8,16….
Here, t1 = 2, t2 = 4, t3 = 8 and t4 = 16
t2 – t1 = 4 – 2 = 2
t3 – t2 = 8 – 4 = 4
t4 – t3 = 16 – 8 = 8
Clearly, the difference of successive terms is not same, therefore given list of numbers does not form an AP.
(vii)
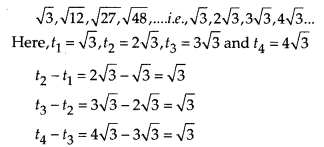
Clearly, the difference of successive terms is same, therefore given list of numbers form an AP.
Question 2.
Justify whether it is true to say that -1, −32, -2, 52 forms an AP as a2 – a1 = a3 – a2.
Solution:
False
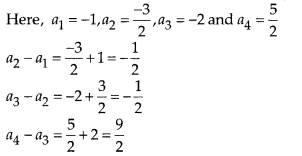
Clearly, the difference of successive terms is not same, all though, a2 – a1 = a3 – a2 but a3 – a2 ≠ a4 – a3, therefore it does not form an AP.
Question 3.
For the AP: -3, -7, -11,can we find directly a30 – a20 without actually finding a30 and a20? Give reasons for your answer.
Solution:
True
∵ nth term of an AP, an = a + (n – 1)d
∴ a30 = a + (30 – 1 )d = a + 29d
and a20 = a + (20 -1)d = a + 19d ………… (i)
Now, a30 – a20 = -(a + 29d) – (a + 19d) = 10d
and from given AP,
Common difference, d = -7 – (-3) = -7 + 3 = -4
∴ a30 – a20 = 10(-4) = -40 [From (i)]
Question 4.
Two APs have the same common difference. The first term of one AP is 2 and that of the other is 7. The difference between their 10th terms is the same as the difference between their 21st terms, which is the same as the difference between any two corresponding terms. Why?
Solution:
Let the same common difference of two AP’s is d. Given that, the first term of first AP and second AP are 2 and 7 respectively, then the AP’s are
2, 2 + d, 2 + 2d, 2 + 3d ….
and 7, 7 + d, 7 + 2d, 7 + 3d ….
Now, 10th terms of first and second AP’s are 2 + 9d and 7 + 9d, respectively
[∵ a10 = a + (10 – 1 )d]
So, their difference is 7 + 9d – (2 + 9d) = 5 Also, 21st terms of first and second AP’s are 2 + 20d and 7 + 20d, respectively
[∵ a21 = a + (21 – 1 )d]
So, their difference is 7 + 20d – (2 + 20d) = 5
Also, if the an and bn are nth terms of first and second AP.
Then, bn – an = [7 + (n – 1 )d)] – [2 + (n – 1)d] = 5
Hence, the difference between any two corresponding terms of such AP’s is the same as the difference between their first terms.
Question 5.
Is 0 a term of the AP: 31, 28, 25, …? Justify your answer.
Solution:
Let 0 be the nth term of given AP i.e., an = 0
Given that, first term a = 31,
common difference, d = 28 – 31 = – 3
The nthterms of an AP, is
an = a + (n – 1 )d
⇒ 0 = 31 + (n – 1)(-3)
⇒ 3(n – 1) = 31
⇒ n – 1 = 313
∴ n = 313+1=343=1113
Since, n should be positive integer. So, 0 is not a term of the given AP.
Question 6.
The taxi fare after each km, when the fare is Rs 15 for the first km and Rs 8 for each additional km, does not form an AP as the total fare (in Rs) after each km is 15, 8, 8, 8,… Is the statement true? Give reasons.
Solution:
Because the total fare (in Rs) after each km is
15, (15 + 8), (15 + 2 × 8), (15 + 3 × 8),…
= 15, 23, 31, 39,…
Let t1 = 15, t2 = 23, t3 = 31 and t4 = 39
Now, t2 – t1 = 23 – 15 = 8
t3 – t2 = 31 – 23 = 8
t4 – t3 = 39 – 31 = 8
Since, all the successive terms of the given list have same difference i.e., common difference is 8. Hence, the total fare after each km form an AP.
Question 7.
In which of the following situations, do the lists of numbers involved form an AP? Give reasons for your answers.
(i) The fee charged from a student every month by a school for the whole session, when the monthly fee is Rs 400.
(ii) The fee charged every month by a school from Classes I to XII, when the monthly fee for Class I is Rs 250, and it increases by Rs 50 for the next higher class.
(iii) The amount of money in the account of Varun at the end of every year when Rs 1000 is deposited at simple interest of 10% per annum.
(iv) The number of bacteria in a certain food item after each second, when they double in every second.
Solution:
(i)The fee charged from a student every month by a school for the whole session is 400, 400, 400, 400,…. which forms an AP, with common difference (d) = 400 – 400 = 0
(ii) The fee charged every month by a school from classes I to XII is
250, (250 + 50), (250 + 2 × 50), (250 + 3 × 50),…
i.e., 250, 300, 350, 400,…
which forms an AP, with common difference (d) = 300 – 250 = 50
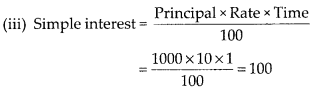
So, the amount of money in the account of Varun at the end of every year is
1000, (1000 + 100 × 1), (1000 + 100 × 2), (1000 + 100 × 3),….
i.e., 1000, 1100, 1200, 1300,….
which forms an AP, with common difference (d) = 1100 – 1000 = 100
(iv) Let the number of bacteria in a certain food = x
Since, they double in every second .-. x, 2x, 2(2x), 2(2 . 2 . x),…
i.e., x, 2x, 4x, 8x,…
Now, let t1 = x, t2 = 2x, t3 = 4x and t4 = 8x
t2 – t1 = 2x – x = x
t3 – t2 = 4x – 2x = 2x
t4 – t3 = 8x – 4x = 4x
Since, the difference between each successsive term is not same. So, the list does form an AP.
Question 8.
Justify whether it is true to say that the following are the nth terms of an AP.
(i) 2n – 3
(ii) 3n2 + 5
(iii) 1 + n + n2
Solution:
Yes. Here an = 2n – 3
Put n = 1, a1 = 2(1) – 3 = -1
Put n = 2, a2 = 2(2) – 3 = 1
Put n = 3, a3 = 2(3) – 3 = 3
Put n = 4, a4 = 2(4) – 3 = 5
List of number becomes -1, 1, 3, 5….
Here, a2 – a1 = 1 – (-1) = 1 + 1 = 2
a3 – a2 = 3 – 1 = 2
a4 – a3 = 5 – 3 = 2
∵ a2 – a1 = a3 – a2 = a4 – a3 = …………
Hence, 2n – 3 is the nth term of an AP.
(ii) No. Here an = 3n2 + 5
Put n = 1, a1 = 3(1)2 + 5 = 8
Put n = 2, a2 = 3(2)2 + 5 = 3(4) + 5 = 17
Put n = 3, a1 = 3(3)2 + 5 = 3(9) + 5 = 27 + 5 = 32
So, the list of number becomes 8, 17, 32,….
Here, a2 – a1 = 17 – 8 = 9
a3 – a2 = 32 -17 = 15
∴ a2 – a1 ≠ a3 – a2
Since, the difference of the successive term is not same,. So, it does not form an AP.
(iii) No. Here an = 1 + n + n2
Put n = 1, a1 = 1 + 1 + (1)2 = 3
Put n = 2, a2 = 1 + 2 + (2)2 = 1 + 2 + 4 = 7
Put n = 3, a3 = 1 + 3 + (3)2 = 1+ 3 + 9 = 13
So, the list of number becomes 3, 7, 13,…
Here, a2 – a1 = 7 – 3 = 4
a3 – a2 = 13 – 7 = 6
∴ a2 – a1 ≠ a3 – a2
Since, the difference of the successive term is not same. So it does not form an AP.
NCERT Exemplar Class 10 Maths Chapter 5 Exercise – 5.3
1. Match the APs given in column A with suitable common differences given in column B

Solution:
(A1) → B4; (A2) → B5; (A3) → B1 and (A4) → B2;
(A1) : 2, -2, -6, -10,…
Here, common difference, d = -2 -2 = -4
(A2) :an = a + (n- 1 )d
⇒ 0 = -18 + (10 – 1)d
18 = 9d
∴ Common difference, d = 2
(A3): fa10 = 6, a = 0
⇒ a + (10 – 1)d = 6 [ ∵ an = a + (n – 1 )d]
⇒ 0 + 9d = 6 [ ∵ a = 0(given)]
d = 69=23
(A4): a2 = 13, a4 = 3
⇒ a + (2 – 1)d = 13 [ ∵ an = a + (n – 1 )d]
⇒ a + d = 13 ………… (i)
and a4 = 3 ⇒ a + (4 – 1)d = 3
∴ a + 3d = 3 …………. (ii)
On subtracting Eq(i) from Eq(ii), we get
2d = -10
⇒ d = 5
Question 2.
Verify that each of the following is an AP, and then write its next three terms.
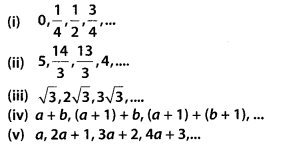
Solution:
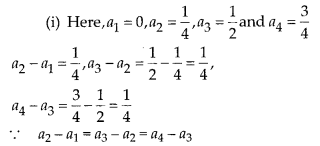
Therefore, the each successive term of the given list has the same difference, So, it forms an AP.
The next three terms are,
Therefore, the each successive term of the given list has same difference.
It forms an AP.
The next three terms are,
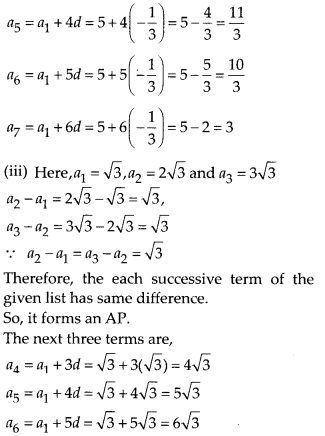
(iv) Here, a1 = a + 6, a2 = (a + 1) + b,
a3 = (a+ 1) + (b +1)
a2 – a1 = (a + 1) + b – (a + b) = a + 1 + b – a – b = 1
a3 – a2 = (a + 1) + (b + 1) — [(a + 1) + b] = a + 1 + b + 1 – a – 1 – b = l
∵ a2 – a1 = a3 – a2 = 1
Therefore, the each successive term of the given list has same difference.
So, it forms an AP.
The next three terms are,
a4 =a1 + 3d = a + b + 3(1) = (a + 2) + (b + 1)
a5 = a1 + 4d = a + b + 4(1) = (a + 2) + (b + 2)
a6 = a1 + 5d = a + b + 5(1) = (a + 3) + (b + 2)
(v) Here, a1 = a, a2 = 2a + 1, a3 = 3a + 2 and a4 = 4a + 3
a2 – a1 = 2a + 1 – a = a + 1
a3 – a2 = 3a + 2 – 2a – 1 = a + 1
a4 – a3 = 4a + 3 – 3a – 2 = a + 1
∵ a2 – a1 = a3 – a2 = a4 – a3 = a + 1
Therefore, the each successive term of the given list has same difference.
So, it forms an AP.
The next three terms are,
a5 = a + 4d = a + 4 (a + 1) = 5a + 4
a6 = a + 5d = a + 5(a + 1) = 6a + 5
a7 = a + 6 d = a + 6 (a + 1) = 7a + 6
Question 3.
Write the first three terms of the APs when a and d are as given below:
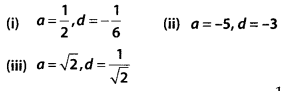
Solution:


Question 4.
Find a, b and c such that the following numbers are in AP: a, 7, b, 23, c.
Solution:
Since a, 7, b, 23, c are in AP.
∴ 7 – a = b – 7 = 23 – b = c – 23
Taking second and third terms, we get
b – 7 = 23 – b
⇒ 2b = 30
∴ b = 15
Taking first and second terms, we get
7 – a = b – 7
⇒ 7 – 8 = 15 – 7 [∵ b = 15]
⇒ 7 – a = 8
∴ a = -1
Taking third and fourth terms, we get
23 – b = c – 23
⇒ 23 – 15 = c – 23 [vh 15]
⇒ 8 = c – 23
⇒ 8 + 23 = c ⇒ c = 31
Hence, a = -1, & = 15, c = 31
Question 5.
Determine the AP whose fifth term is 19 and the difference of the eighth term from the thirteenth term is 20.
Solution:
Let the first term of an AP be a and common difference d.
Given, a5 = 19 and a13 – a8 = 20 [given]
∴ a5 = a + (5 – 1)d = 19 and
[a + (13 – 1 )d] – [a + (8 – 1 )d] = 20
[∵ an = a + (n- 1 )d]
⇒ a + 4d = 19 …………. (i)
and a + 12d – a – 7d = 20 ⇒ 5d = 20
∴ d = 4
On putting d = 4 in Eq. (i), we get
a + 4(4) = 19
8 + 16 = 19
8 = 19 – 16 = 3
So, required AP is a, a + d, a + 2d, a + 3d …. i.e.,
3, 3 + 4, 3 + 2(4), 3 + 3(4),…. i.e., 3, 7, 11, 15, …
Question 6.
The 26th, 11th and the last term of an AP are 0, 3 and −15 respectively. Find the common
difference and the number of terms.
Solution:
Let the first term, common difference and number of terms of an AP are a, d and n, respectively.
We know that, if last term of an AP is known, then
l = 8 + (11-1 )d …………. (i)
and nth term of an AP is
Tn = a + (n – 1)d …………. (ii)
Given that, 26th term of an AP = 0
⇒ T26 = a + (26 – 1 )d = 0 [from Eq.(i)]
⇒ 8 + 25d = 0 …………. (iii)
11th term of an AP = 3
⇒ T11 = s + (11 – 1)d = 3 [from Eq.(ii)]
⇒ 8 + 10d = 3 ……………… (iv)
and last term of an AP = -1/ 5
⇒ l = a + (n – 1 )d [from Eq (i)]
⇒ -1/5 = a + (n – 1 )d ………… (v)
Now, subtracting Eq(iv) from Eq(iii),
15 d = – 3
⇒ d = −15
Put the value of d in Eq.(iii), we get
a + 25(−15) = 0
⇒ a – 5 = 0 ⇒ 8 = 5
Now put the value of a, d in Eq. (v), we get
-1/5 = 5 + (n – 1)(-1/5)
⇒ -1 = 25 – (n – 1)
⇒ -1 = 25 – n + 1
⇒ n = 25 + 2 = 27
Hence, the common difference and number of terms are -1/ 5 and 27, respectively.
Question 7.
The sum of the 5th and the 7th terms of an AP is 52 and the 10th term is 46. Find the AP.
Solution:
Let the first term and common difference of AP are a and d, respectively.
According to the question,
a5 + a7 = 52 and a10 = 46
⇒ a + (5 – l)d + a + (7 – 1)d = 52
[∵ an = a + (n- 1 )d]
and a + (10 – 1 )d = 46
⇒ a + 4d + a + 6d = 52
and a + 9d = 46
⇒ 2a + 10d = 52
and a + 9d = 46
⇒ a + 5d = 26 ………….. (i)
a + 9d = 46 ……………. (ii)
On subtracting Eq. (i) from Eq. (ii), we get
4d = 20 ⇒ d = 5 From Eq. (i) a = 26 – 5(5) = 1
So, required AP is a, a + d, a + 2d, a + 3d …. i.e., 1, 1 + 5, 1 + 2(5), 1 + 3(5)… i.e., 1, 6,11,16,….
Question 8.
Find the 20th term of the AP whose 7th term is 24 less than the 11th term, first term being 12.
Solution:
Let the first term, common difference and number of terms of an AP are a, d and n, respectively.
Given that, first term (a) = 12 Now by given condition,
7th term (T7) = 11th term (T11) – 24
[∵ nth term of an AP, Tn = a + (n – 1 )d]
⇒ a + (7 – 1)d = a + (11 – l)d – 24
⇒ a + 6d = a + 10d – 24
⇒ 24 = 4d ⇒ d = 6
∴ 20th term of AP, T20 = a + (20 – 1)d
= 12 + 19 × 6 = 126
Hence, the required 20th term of an AP is 126.
Question 9.
If the 9th term of an AP is zero, prove that its 29th term is twice its 19th term.
Solution:
Let the first term, common difference and number of terms of an AP are a, d and n respectively.
Given that, 9th term of an AP, i.e., T9 = 0
[∵ nth term of an AP, Tn = a + (n – 1 )d]
⇒ a + (9 – 1)d = 0
⇒ a + 8d = 0 ⇒ a = -8 d ………….. (i)
Now, its 19th term, T19 = a + (19 – 1)d
= -8d + 18d [From Eq.(i)]
= 10d …………… (ii)
and its 29th term, T29 = a + (29 – 1)d
= -8d + 28d = 20d = 2 × (10d)
[from Eq.(i)]
⇒ T29 = 2 × T19
Hence, its 29th term is twice its 19th term.
Question 10.
Find whether 55 is a term of the AP: 7, 10, 13,— or not. If yes, find which term it is.
Solution:
Yes. Let the first term, common difference and the number of terms of an AP are a, d and n respectively.
Let the nth term of an AP be 55. i.e., Tn = 55
We know that, the nth term of an AP,
Tn = a + (n – 1 )d …………….. (i)
Given that, first term (a) = 7
and common difference (d) = 10 – 7 = 3
From Eq. (i), 55 = 7 + (n – 1) × 3
⇒ 55 = 7 + 3M – 3 = 4 + 3n
⇒ 3n = 51
∴ n = 17
Since, n is a positive integer. So 55 is a term of the AP.
Since, n = 17
Therefore, 17th term of an AP is 55.
Question 11.
Determine k so that k2+ 4k + 8, 2k2 + 3k + 6, 3k2 + 4k + 4 are three consecutive terms of an AP.
Solution:
Since, k2 + 4k + 8, 2k2 + 3k + 6 and 3k2 + 4k+ 4 are consecutive terms of an AP.
∴ 2k2+ 3k + 6- (k2 + 4k + 8)
= 3k2 + 4k + 4 – (2k2 + 3k + 6) = Common difference
⇒ 2k2 + 3k + 6 – k2 – 4k – 8 = 3k2 + 4k + 4 – 2k2 – 3k – 6
⇒ k2 – k – 2 = k2 + k – 2
⇒ -k = k ⇒ 2k = 0 ⇒ k = 0
Question 12.
Split 207 into three parts such that these are in AP and the product of the two smaller parts is 4623.
Solution:
Let the three parts of the number 207 are (a – d), a and (a + d), which are in AP.
Now, by given condition,
⇒ Sum of these parts = 207
⇒ a – d + a + a + d = 207
⇒ 3a = 207
a = 69
Given that, product of the two smaller parts = 4623
⇒ a(a -d) = 4623
⇒ 69 . (69 – d) = 4623
⇒ 69 – d = 67
⇒ d = 69 – 67 = 2
So, first part = a – d = 69 – 2 = 67,
Second part = a = 69
and third part = n + d = 69 + 2 = 71
Hence, required three parts are 67, 69, 71.
Question 13.
The angles of a triangle are in AP. The greatest angle is twice the least. Find all the angles of the triangle.
Solution:
Given that, the angles of a triangle are in AP.
Let A, B and C are angles of a ∆ABC
B = A+C2
⇒ 2B = A + C …(i)
We know that, sum of all interior angles of a ∆ABC is 180° ’
A + B + C = 180°
⇒ 2B + B = 180° [from Eq(i)]
⇒ 3B = 180°
⇒ B = 60°
Let the greatest and least angles are A and C respectively
A = 2C [by condition] …………. (ii)
Now, put the values of B and A in Eq(i), we get
2 × 60° = 2C + C
⇒ 120° = 3 C
⇒ C = 40°
Put the value of C in Eq(ii), we get
A = 2 × 40°
⇒ A = 80°
Hence, the required angles of a triangle are 80°, 60° and 40°.
Question 14.
If the nth terms of the two APs: 9, 7, 5,… and 24, 21, 18,. .. are the same, find the value of n. Also find that term.
Solution:
Let the first term, common difference
and number of terms of the AP: 9, 7, 5,…. are
a1, d1 and n1, respectively
i.e., first term (a1) = 9
and common difference (d1) = 7 – 9 = -2
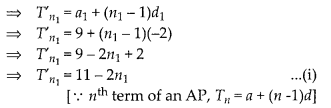
Let the first term, common difference and the number of terms of the AP: 24, 21, 18, … are a2, d2 and n2, respectively
i.e., first term, (a2) = 24
and common difference (d2) = 21 – 24 = -3

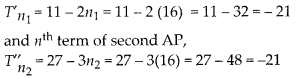
Hence, the value of n is 16 and that term i.e., nth term is -21.
Question 15.
If sum of the 3rd and the 8th terms of an AP is 7 and the sum of the 7th and the 14th terms is -3, find the 10th term.
Solution:
Let the first term and common difference of an AP are a and d, respectively.
According to the questiuon,
a3 + a8 = 7 and a17 + a14 = -3
⇒ a + (3 – 1)d + a + (8 – 1)d = 7
[∵ an = a + (n- 1 )d]
and a + (7 – 1 )d + a + (14 – 1 )d = -3
⇒ a + 2d + a + 7d = 7
and a + 6d + a + 13d = -3
⇒ 2A + 9d = 7 ………….. (i)
and 2a + 19d = -3 …(ii)
On subtracting Eq(i) from Eq(ii), we get
10d = -10 ⇒ d = -1
2a + 9(-1) = 7 [from Eq(i)]
⇒ 2a – 9 = 7
⇒ 2a = 16
⇒ a = 8
∴ a10 = a + (10 – 1)d
= 8 + 9(-1) = 8 – 9 = -1
Question 16.
Find the 12th term from the end of the AP: -2, -4,-6, …,-100.
Solution:
Given AP : -2, -4, -6,…., -100
Here, first term (a) = -2,
common difference (d) = -4 – (-2) = -2
and the last term (l) = -100
We know that, the nth term of an AP from the
end an = l – (n – 1 )d, where l is the last term
and d is the common difference.
∴ 12th term from the end, i.e.,
a12 = -100 – (12 – 1)(-2)
= -100 + (11)(2) = -100 + 22 = -78
Hence, the 12th term from the end is -78
Question 17.
Which term of the AP: 53, 48, 43,… is the first negative term?
Solution:
Given AP is 53, 48, 43,…
whose first term (a) = 53 and
common difference (d) = 48 – 53 = -5
Let nth term of the AP be the first negative term.
i.e., Tn < 0
[∵ nth term of an AP, Tn = a + (n – 1)d]
⇒ [a + (n – 1 )d] < 0
⇒ 53 + (n – 1)(-5) < 0
⇒ 53 – 5n + 5 < 0
⇒ 58 – 5n < 0 ⇒ 5n > 58
⇒ n > 11.6 ⇒ n = 12
i.e., 12th term is the first negative term of the given AP
∴ T12 = a + (12 – 1)d = 53 + 11 (-5)
= 53 – 55 = – 2 < 0
Question 18.
How many numbers lie between 10 and 300, which when divided by 4 leave a remainder 31
Solution:
Here, the first number is 11, which divided by 4 leave a remainder 3 between 10 and 300
Last term before 300 is 299, which divided by 4 leave remainder 3.
∴ 11, 15, 19, 23, 299
Here, first term (a) = 11,
common difference (d) = 15 – 11 = 4
[∵ nth term, an = a + (n – 1)d]
⇒ 299 = 11 + (n – 1) 4
⇒ 4(n – 1) = 288
⇒ (n – 1) = 72
∴ n = 73
Question 19.
Find the sum of the two middle most terms of theAP: −43,−1,−23,…,413
Solution:

and a10 = −43+9(13)=9−43=53
So, sum of the two middle most terms
= a9 + a10 = 43+53=93=3
Question 20.
The first term of an AP is -5 and the last term is 45. If the sum of the terms of the AP is 120, then find the number of terms and the common difference.
Solution:
Let the first term, common difference and the number of terms of an AP are a, d and n respectively.
Given that, first term (a) = -5 and
last term (l) = 45
Sum of the terms of the AP = 120 ⇒ Sn = 120
We know that, if last term of an AP is known, then sum of n terms of an AP is,
Sn = n2 (a + l)
⇒ 120 = n2(-5 + 45) ⇒ 120 × 2 = 40 × n
⇒ n = 3 × 2 ⇒ n = 6
∴ Number of terms of an AP is known, then the nth term of an AP is,
l = a + (n – 1)d ⇒ 45 = -5 + (6 – 1)d
⇒ 50 = 5d ⇒ d = 10
So, the common difference is 10.
Hence, number of terms and the common difference of an AP are 6 and 10 respectively.
Question 21.
Find the sum:
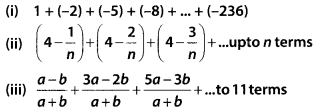
Solution:
(i) Here, first term (a) = 1 and common difference (d) = (-2) – 1 = -3
∵ Sum of n terms of an AP,
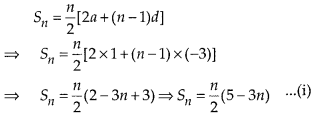
We know that, if the last term (l) of an AP is known, then
l = a + (n – 1)d
⇒ -236 = 1 + (n – 1) (-3) [∵ l = -236, given]
⇒ -237 = -(n – 1) × 3
⇒ n – 1 = 79 ⇒ n = 80
Now, put the value of n in Eq(i), we get on
Sn = 802 [5 – 3 × 80] = 40[5- 240]
= 40 × (-235) = -9400
Here, the required sum is -9400


Question 22.
Which term of the AP: -2, -7, -12,… will be -77? Find the sum of this AP upto the term -77.
Solution:
Given, AP : -2, -7, -12, ….
Let the nth term of an AP is -77
Then, first term (a) = -2 and
common difference (d) = -7 – (-2) = -7 + 2 = -5
∵ nth term of an AP, Tn = a + (n – 1)d
⇒ -77 = -2 + (n – 1)(-5)
⇒ -75 = -(n – 1) × 5
⇒ (n – 1) = 15 ⇒ n = 16
So, the 16th term of the given AP will be -77
Now, the sum of n terms of an AP is
Sn = n2 [2a + (n – 1)d]
So, sum of 16 terms i.e., upto the term -77
S16 = 162 [2 × (-2) + (n – 1)(-5)l
= 8[-4 + (16 – 1)(-5)] = 8(-4 – 75)
= 8 × (-79)= -632
Hence, the sum of this AP upto the term -77 is -632.
Question 23.
If an = 3 – 4n, show that a1, a2, a3,… form an AP. Also find S20
Solution:
Given that, nth term of the series is
an = 3 – 4n …(i)
Put n = 1, a1 = 3 – 4(1) = 3 – 4 = -1
Put n = 2, a2 = 3 – 4(2) = 3 – 8 = -5
Put n = 3, a3 = 3 – 4(3) = 3 – 12 = -9
Put n = 4, a4 = 3 – 4(4) = 3 – 16 = -13
So, the series becomes -1, -5, -9, -13,….
We see that,
a2 – a1 = -5 – (-1) = -5 + 1 = -4,
a3 – a2 = -9- (-5) = -9 + 5 = -4,
a4 – a3 = -13 – (-9) = -13 + 9 =-4
i.e., a2 – a1 = a3 – a2 = a4 – a3 = … = —4
Since, the each successive term of the series has the same difference. So, it forms an AP. We know that, sum of n terms of an AP,
Sn = n2 [2a + (n – 1)d]
∴ Sum of 20 terms of the AP,
S20 = 202 [2(-1) + (20 – 1)(-4)]
= 10 [-2 + (19)(-4)] = 10(-2 – 76)
= 10 × (-78) = -780
Hence, the required sum of 20 terms i.e., S20 is -780
Question 24.
In an AP, if Sn = n (4n + 1), find the AP.
Solution:
We know that, the nth term of an AP is
an = Sn – Sn – 1
an = n(4n + 1) – (n – 1) {4(n -1) + 1}
[∵ Sn = n (4n + 1)]
⇒ an = 4n2 + n- (n – 1)(4 n – 3)
= 4n2 + n – 4n2 + 3n + 4n – 3 = 8n – 3
Put n = 1, a1 = 8(1) -3 = 5
Put n = 2, a2 = 8(2) – 3 = 16 – 3 = 13
Put n = 3, a3 = 8(3) – 3 = 24 – 3 = 21
Hence, the required AP is 5, 13, 21,….
Question 25.
In an AP, if Sn = 3n2 + 5n and ak = 164, find the value of k.
Solution:
∵(nth term of an AP,
an = Sn – Sn – 1
= 3n2 + 5n – 3(n – 1)2 – 5(w – 1)
[∵ Sn = 3n2 + 5n (given)]
= 3n2 + 511 – 3n2 – 3 + 6n – 5n + 5
⇒ an = 6n + 2 …………… (i)
or ak = 6k + 2 = 164 [∵ ak = 164 (given)]
⇒ 6k = 164 – 2 = 162
∴ k = 27
Question 26.
If Sn denotes the sum of first n terms of an AP, prove that S12 = 3(S8 – S4).
Solution:
Sum of n terms of an AP,

Question 27.
Find the sum of first 17 terms of an AP whose 4th and 9th terms are -15 and -30 respectively.
Solution:
Let the first term, common difference and the number of terms in an AP are a, d and n, respectively.
We know that, the nth term of an AP,
Tn = a + (n – 1)d …………….. (i)
∴ 4th term of an AP,
T4 = a + (4 – 1)d = -15 [given]
⇒ a + 3d = -15 ………………. (ii)
and 9th term of an AP,
T9 = a + (9 – 1)d = -30 [given]
⇒ a + 8d = -30 …………. (iii)
Now, subtract Eq. (ii) from Eq. (iii), we get
5d = -15
⇒ d = -3
Put the value of d in Eq.(ii), we get
a + 3(-3) = -15
⇒ a – 9 = -15 ⇒ a = -15 + 9 = – 6
∵ Sum of first n terms of an AP,

Hence, the required sum of first 17 terms of an AP is -510.
Question 28.
If sum of first 6 terms of an AP is 36 and that of the first 16 terms is 256, find the sum of first 10 terms.
Solution:
Let a and d be the first term and common difference, respectively of an AP.
∵ Sum of n terms of an AP,
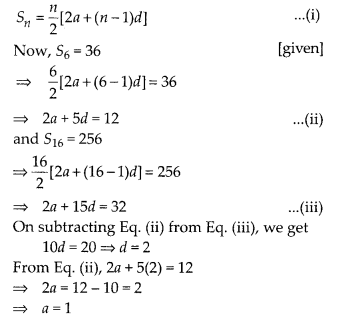
∴ S10 = 102 [2a + (10 – 1)d]
= 5[2(1) + 9(2)] = 5(2 + 18) = 5 × 20 = 100
Hence, the required sum of first 10 terms is 100.
Question 29.
Find the sum of all the 11 terms of an AP whose middle most term is 30.
Solution:
Since, the total number of terms (n) = 11 [odd]
∴ Middle most term
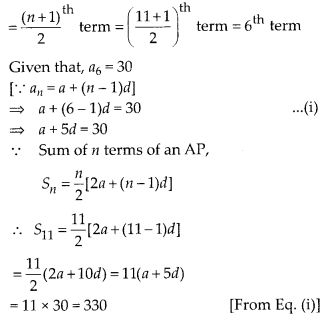
Question 30.
Find the sum of last ten terms of the AP: 8,10, 12,……., 126.
Solution:
For finding the sum of last ten terms, we write the given AP in reverse order.
i.e., 126, 124, 122,…., 12, 10, 8
Here, first term (a) = 126,
common difference (d) = 124 – 126 = – 2
∴ S10 = 102 [2a + (10 – 1)d]
[∵ Sn = n2 [2a + (n – 1)d]]
= 5{2(126) + 9(—2)} = 5(252 – 18)
= 5 × 234 = 1170
Question 31.
Find the sum of first seven numbers which are multiples of 2 as well as of 9.
Solution:
For finding the sum of first seven numbers which are multiples of 2 as well as of 9. Take LCM of 2 and 9 which is 18.
So, the series becomes 18, 36, 54 ….
Here, first term (a) = 18,
common difference d) = 36 – 18 = 18
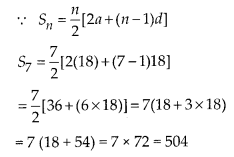
Question 32.
How many terms of the AP: -15, -13, -11,— are needed to make the sum -55? Explain the reason for double answer.
Solution:
Let n number of terms are needed to make the sum -55
Here, first term (a) = -15,
common difference (d) = -13 + 15 = 2
∵ Sum of n terms of an AP,
Sn = n2 [2a + (n – 1)d]
⇒ -55 = n2 [2(-15) + (n – 1)2]
[∵ Sn = -55 (given)]
⇒ -55 = -15M + n(n – 1)
⇒ n2 – 16n + 55 = 0
⇒ n2 – 11n – 5n + 55 = 0
[by factorisation method]
⇒ n(n – 11) – 5(n – 11) = 0
⇒ (n – 11)(n – 5) = 0
∴ n = 5, 11
Hence, either 5 or 11 terms are needed to make the sum -55 when n = 5,
AP will be -15, -13, -11, -9, -7,
So, resulting sum will be -55 because all terms are negative.
When n = 11,
AP will be -15, -13, -11, -9, -7, -5, -3, -1, 1, 3, 5
So resulting sum will be -55 because the sum of terms 6th to 11th is zero.
Question 33.
The sum of the first n terms of an AP whose first term is 8 and the common difference is 20 is equal to the sum of first 2n terms of another AP whose first term is – 30 and the common difference is 8. Find n.
Solution:
Given that, first term of the first AP (a) = 8
and common difference of the first AP(d) = 20
Let the number of terms in first AP be n.
∵ Sum of first n terms of an AP,
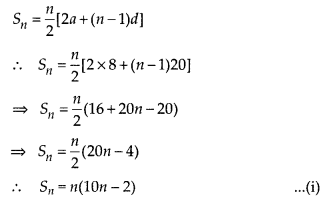
Now, first term of the second AP(a’) = – 30 and common difference of the second AP(d’) = 8
∴ Sum of first 2n terms of second AP,
S2n = 2n2 [2a’ + (2n – 1)d’]
⇒ S2n = n[2(-30)+(2n – 1)(8)]
⇒ S2n = n[-60 + 16n – 8)]
⇒ S2n = n[16n – 68] ………… (ii)
Now, by given condition,
Sum of first n terms of the first AP = Sum of first 2n terms of the second AP
⇒ Sn — S2n
⇒ n(10n – 2) = n(16n – 68)
[from Eqs.(i) and (ii)]
⇒ n[(16n – 68) – (10n – 2)] = 0
⇒ n(16n – 68 – 10n + 2) = 0
⇒ n(6n – 66) = 0
⇒ n = 11 [∵ n ≠ 0]
Hence, the required value of n is 11.
Question 34.
Kanika was given her pocket money on Jan 1st, 2008. She puts ₹ 1 on Day 1, ₹ 2 on Day 2, ₹ 3 on Day 3, and continued doing so till the end of the month, from this money into her piggy bank. She also spent ₹ 204 of her pocket money and found that at the end of the month she still had ₹ 100 with her. How much was her pocket money for the month?
Solution:
Let her pocket money be ₹ x
Now, she puts 11 on day 1, ₹ 2 on day 2, ₹ 3 on day 3 and so on till the end of the month, from this money into her piggy bank.
i.e., 1 + 2 + 3 + 4 + … + 31
which form an AP in which terms are 31 and first
term (a) = 1, common difference (d) = 2 – 1 = 1
∴ Sum of first 31 terms is S31
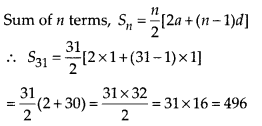
So, Kanika takes ₹ 496 till the end of the month from this money.
Also, she spent ₹ 204 of her pocket money and found that at the end of the month she still has ₹ 100 with her.
Now, according to the condition,
(x – 496) – 204 = 100
⇒ x – 700 = 100
∴ x = ₹ 800
Hence, ₹ 800 was her pocket money for the month.
Question 35.
Yasmeen saves ₹ 32 during the first month, ₹ 36 in the second month and ₹ 40 in the third month. If she continues to save in this manner, in how many months will she save Rs 2000?
Solution:
Given that,
Yasmeen, during the first month, saves = ₹ 32
During the second month, saves = ₹ 36
During the third month, saves = ₹ 40
Let Yasmeen saves Rs 2000 during the n months.
Here, we have arithmetic progression 32, 36, 40,…
First term (a) = 32,
common difference (d) = 36 – 32 = 4
and she saves total money, i.e., Sn = ₹ 2000
We know that, sum of first n terms of an AP is,
Sn = n2[2a + (n – 1)d]
⇒ 2000 = n2 [2 × 32 + (n -1) × 4]
⇒ 2000 = n(32 + 2n – 2)
⇒ 2000 = n(30 + 2n)
⇒ 1000 = n (15 + n)
⇒ 1000 = 15n + n2
⇒ n2 + 15n – 1000 = 0
⇒ n2 + 40n – 25n – 1000 = 0
⇒ n(n + 40) – 25(n + 40) = 0
⇒ (n + 40)(n – 25)= 0
∴ n = 25 [ ∵ n ≠ – 40]
[since, months cannot be negative]
Hence, in 25 months she will save ₹ 2000.
NCERT Exemplar Class 10 Maths Chapter 5 Exercise – 5.4
Question 1.
The sum of the first five terms of an AP and the sum of the first seven terms of the same AP is 167. If the sum of the first ten terms of this AP is 235, find the sum of its first twenty terms.
Solution:
Let the first term, common difference and the number of terms of an AP are a, d and n, respectively.
∵ Sum of first n terms of an AP,

Now, by given condition,
S5 + S7 = 167
⇒ 5a + 10 d + 7a + 21 d = 16 7
⇒ 12a + 31d = 167 ………..(iv)
Given that, sum of first ten terms of this AP is 235.
∴ S10 = 235
⇒ 102 [2a + (10 – l)d] = 235
⇒ 5(2a + 9d) = 235
⇒ 2a + 9d = 47 …(v)
On multiplying Eq(v) by 6 and then subtracting it into Eq(iv), we get
23d = 115
⇒ d = 5
Now, put the value of d in Eq(v), we get
2a + 9(5) = 47 ⇒ 2a + 45 = 47
⇒ 2a = 47 – 45 = 2 ⇒ a = 1
Sum of first twenty terms of this AP,
S20 = 202 [2a + (20 – 1)d]
= 10[2 × (1) + 19 × (5)] = 10(2 + 95)
= 10 × 97 = 970
Hence, the required sum of its first twenty terms is 970.
Question 2.
Find the
(i) Sum of those integers between 1 and 500 which are multiples of 2 as well as of 5.
(ii) sum of those integers from 1 to 500 which are multiples of 2 as well as of 5.
(iii) sum of those integers from 1 to 500 which are multiples of 2 or 5.
Solution:
(i) Since, multiples of 2 as well as of 5
= LCM of (2, 5) = 10
∴ Multiples of 2 as well as of 5 between 1
and 500 is 10, 20, 30,…, 490
which form an AP with first term (a) = 10 and
common difference (d) = 20 – 10 = 10
nth term an = Last term (l) = 490
∴ Sum of n terms between 1 and 500,
Sn = n2 [a + l] …………. (i)
[∵ an = a + (n – 1)d = l]
⇒ 10 + (n – 1) 10 = 490
⇒ (n -1)10 = 480
⇒ n — 1 = 48 ⇒ n = 49
From Eq (i), S49 = 492 (10 + 490)
= 492 × 500 = 49 × 250 = 12250
(ii) Same as part (i),
But multiples of 2 as well as 5 from 1 to 500 is 10, 20, 30,…, 500.
∴ a = 10, d = 10, an = l = 500
∵ an = a + (n – 1)d = 1
⇒ 500 = 10 + (n- 1)10
⇒ 490 = (n – 1) 10
⇒ n – 1 = 49
⇒ n = 50
∵ Sn = n2 (a + l)
⇒ S50 = 502 (10 + 500) = 502 × 510
= 50 × 255 = 12750
(iii) Since, multiples of 2 or 5 = Multiples of 2 + Multiples of 5 – [Multiples of LCM (2,5) i.e., 10],
∴ Multiples of 2 or 5 from 1 to 500
= List of multiples of 2 from 1 to 500 + List of multiples of 5 from 1 to 500 – List of multiples of 10 from 1 to 500
= (2, 4, 6,…, 500) + (5, 10,15,…, 500) – (10, 20,…, 500) ………. (i)
All of these list form an AP.
Now, number of terms in first list,
500 = 2 + (n1 – 1)2 ⇒ 498 = (n1 -1)2
[∵ a1 = a + (n – 1)d]
⇒ n1 – 1 = 249 ⇒ n1 = 250
Number of terms in second list,
500 = 5 + (n2 – 1)5 ⇒ 495 = (n2 – 1)5
[∵ l = 500]
⇒ 99 = (n2 – 1) ⇒ n2 = 100
and number of terms in third list,
500 = 10 + (n3 – 1)10 ⇒ 490 = (n3 – 1)10
⇒ n3 – 1 = 49 ⇒ n3 = 50
From Eq(i) Sum of multiples of 2 or 5 from 1 to 500
= Sum of (2, 4, 6, …500) + sum of (5,10,…, 500) – Sum of (10, 20,…, 500)
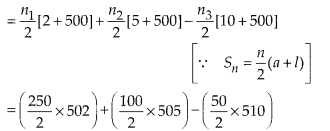
= (250 × 251) + (505 × 50) – (25 × 510)
= 62750 + 25250 -12750 = 88000 -12750 = 75250
Question 3.
The eighth term of an AP is half its second term and the eleventh term exceeds one third of its fourth term by 1. Find the 15th term.
Solution:
Let a and d the first term and common difference of an AP, respectively
Now, by given condition, a8 = 12 a2
⇒ a + 7d = 12 (a + d) [∵ an = a + (n – 1 )d]
⇒ 2a + 14d = a + d
⇒ a + 13d = 0 …………. (i)
and a11 = 13 a4 + 1 [given]
⇒ a + 10d = 13 [a – 3d] + 1
⇒ 3 a + 30d = a + 3d + 3
⇒ 2a + 27d = 3
From Eqs. (i) and (ii)
2(-13d) + 27d = 3
⇒ -26d + 27d = 3
⇒ d = 3
From Eq. (i),
a + 13(3) = 0
⇒ a = -39
∴ a15 = a + 14d = -39 + 14(3) = -39 + 42 = 3
Question 4.
An AP consists of 37 terms. The sum of the three middle most terms is 225 and the sum of the last three is 429. Find the AP.
Solution:
Since, total number of terms (n) = 37 [odd]
∴ Middle term = (37+12)th term = 19th term
So, the three middle most terms = 18th, 19th and 20th,
By given condition.
Sum of the three middle most terms = 225
a18 + a19 + a20 = 225
⇒ (a + 17d) + (a + 18d) + (a + 19 d) = 225
[∵ an = a + (n – 1 )d]
⇒ 3a + 54d = 225
⇒ a + 18d = 75 …………. (i)
and sum of the last three terms = 429
⇒ a35 + a36 + a37 = 429
⇒ (a + 34d) + (a + 35d) + (a + 36 d) = 429
⇒ 3a + 105d = 429
⇒ a + 35d = 143 ………….. (ii)
On subtracting Eq.(i) from Eq. (ii), we get
17d = 68
⇒ d = 4
From Eq. (i), a + 18(4) = 75
⇒ a = 75 – 72
⇒ a = 3
∴ Required AP is a, a + d, a + 2d, a + 3d,….
i.e., 3, 3 + 4, 3 + 2(4), 3 + 3(4),…
i.e., 3, 7, 3 + 8, 3 + 12,….
i.e., 3, 7, 11, 15,….
FAQ’s
Q. What are the types of questions in NCERT Exemplar Solutions for Class 10 Maths Chapter 5?
Ans: Multiple choice questions, descriptive type questions, long answer type questions, short answer type questions, fill in the gaps, and daily life examples are included in Chapter 5 of NCERT Exemplar Solutions for Class 10 Maths. Students will be able to improve their problem-solving and time management skills by the end of this chapter. This helps them get good grades in their CBSE Term II exams.
Q. Is it required to learn all of the concepts covered in Chapter 5 of the NCERT Exemplar Solutions for Class 10 Maths?
Ans: Yes, learning all of the subjects in NCERT Exemplar Solutions for Class 10 Maths Chapter 5 is required in order to achieve excellent results in the second term exams. These solutions were created by subject matter specialists who compiled model questions that covered all of the textbook’s exercise questions. They also concentrate on deciphering math solutions in a simple style for kids to comprehend.
Q. Is it possible to use the NCERT Exemplar Solutions for Class 10 Maths Chapter 5 to answer all of the questions in the CBSE Term II exams?
Ans: Yes, using the NCERT Exemplar Solutions for Class 10 Maths Chapter 5 to answer all of the problems in the CBSE Term II exams is sufficient. These questions were created using the most recent CBSE term-by-term syllabus and guidelines. As a result, the pupils do well in the CBSE final second-term examination. By rehearsing this chapter, they will be able to grasp the principles with ease.



