
Courses

By Shailendra Singh
|
Updated on 20 Nov 2024, 13:21 IST
The resistance of a fluid (liquid or gas) to a change in shape or movement of neighbouring portions relative to one another is referred to as viscosity. Viscosity denotes resistance to flow. Fluidity is a measure of how easily a substance flows and is defined as the reciprocal of viscosity. The viscosity of molasses, for example, is higher than that of water.
Internal friction between molecules can be thought of as viscosity; this friction opposes the development of velocity differences within a fluid since a section of a fluid that is compelled to move carries along nearby parts to some extent. Viscosity is a crucial component in determining the forces that must be overcome when fluids are employed in lubrication and transferred in pipes. It regulates liquid flow in processes such as spraying, injection moulding, and surface coating.
The rate of shear strain, or rate of deformation, is precisely related to the tangential, or shearing, stress that generates flow in many fluids. In other words, the shear stress divided by the rate of shear strain is constant for a given fluid at a set temperature.
The dynamic, or absolute, viscosity, or simply the viscosity, is the name given to this constant. Fluids that behave in this manner are known as Newtonian fluids, after Sir Isaac Newton, who first developed this mathematical description of viscosity. Dynamic viscosity has the dimensions force-time area. As a result, the unit of viscosity is newton-second per square metre, which is usually expressed in SI units as pascal-second. In some cases, kinematic viscosity is more valuable than absolute or dynamic viscosity.
The absolute viscosity of a fluid is divided by its mass density to get kinematic viscosity.
Kinematic viscosity is defined as area divided by time; the appropriate units are metre squared per second. The centimetre-gram-second (CGS) system’s unit of kinematic viscosity, known as the stokes in the United Kingdom and the stoke in the United States, is named after British physicist Sir George Gabriel Stokes. One stoke equals one centimetre squared per second.
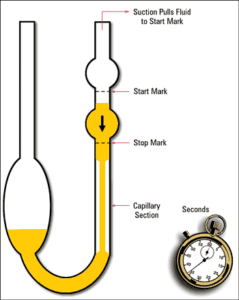
Viscosity is a concept that describes the struggle of fluid against a flowing that is distorted due to extensional stress forces or shear stress. Kinematic viscosity is calculated by dividing the fluid mass density by the dynamic fluid, viscosity, or absolute fluid viscosity. Momentum diffusivity is a term that is used from time to time. Kinematic viscosity units are based on time and area. It is the ratio of dynamic viscosity to density, which is a force-independent quantity. It is the time area ratio; henceforth, it is m²/s or ft²/s.
The kinematic viscosity formula is as follows: ν = μ/ρ

Kinematic Viscosity’s dimensional formula is given by,
M0 L2 T-1
Where,
M stands for mass.
T = Time, L = Length
Kinematic viscosity (ν) = Dynamic viscosity × [Density]-1. . . . (1)

Density = Mass × [Volume]-1
⇒ ρ = [M1 L0 T0] × [M0 L3 T0]-1
The density dimensional formula = [M1 L-3 T0] . . . . (2)
Dynamic viscosity (η) = Tangential Force × distance between layers × [Area × velocity]-1 . . . . . (3)
Tangential Force = M × a = M × [L T-2]
The dimensions of force = M1 L1 T-2 . . . . (4)
The area and velocity dimensional formula = L2 and L1 T-1 . . . . (5)
When we substitute equations (4) and (5) into equation (3), we get
Dynamic viscosity (η) = [M L T-2] × [L] × [L2]-1 × [L1 T-1]-1 = [M1 L-1 T-1].
The dynamic viscosity dimensions = [M1 L-1 T-1] . . . .(6)
When we substitute equations (2) and (6) into equation (1), we get
Kinematic viscosity (ν) = Dynamic viscosity × [Density]-1
Or, ν = [M1 L-1 T-1] × [M1 L-3 T0]-1 = [M0 L2 T-1].
Kinematic viscosity is represented dimensionally as [M0 L2 T-1].
The kinematic viscosity of a liquid is defined as its absolute viscosity divided by its density at the same temperature.
Kinematic viscosity units are based on time and area. It is the ratio of dynamic viscosity to density, which is a force-independent quantity. It is the time area ratio; henceforth, it is m22/s or ft22/s. The kinematic viscosity formula is written as ν = μ/ρ