Dimension of Kinetic Energy

Intorduction to Dimension of Kinetic Energy

Motor energy is characterized as the energy that is created by an article because of its movement. At the point when an item is set to speed increase, there is a positive need to apply specific powers. The utilization of power needs work, and after the work is done, the energy gets moved to the item making it move at a consistent speed.

Here, the energy moved is alluded to as dynamic energy and relies upon the speed and mass of the item being gotten underway.

Fun Facts: As we push forward on this page, you will see the way energy in an article changes starting with one structure and then onto the next.

For example, take a flying squirrel that has crashed into a chipmunk in its rest state. After the crash, there will be a progression of motor energy bringing about the squirrel to change its energy into a few different structures. It will stop and afterward the motor energy will be zero.

How Might We Calculate Kinetic Energy?

To figure out the active energy, there should be some thinking stage. A portion of the discoveries are required, similar to the work done (W), forcibly (F). Along these lines, for example, consider a crate of mass m that is being pushed to a distance d in light of the utilization of a power corresponding to the surface.

Taking a gander at the meaning of work done, it is the result of power and distance.

W​=F⋅d

=m⋅a⋅d​

From the kinematic conditions of movement, it is expressed that we could substitute the speed increase an if the underlying and last speed v and v0​ and the distance d. Is given:

Along these lines, from that, we determine:

v² =v²₀ +2ad

gives us,

a= (v² + v²₀ ) / 2ad

At the point when a net measure of work is done, the motor energy K changes.

Motor Energy

K= (mv² )/ 2

All in all, the adjustment of motor energy is equivalent to the net work done on a framework or an item.

W_net =△K

The previously mentioned equation is supposed to be the work-energy hypothesis and applies from an overall perspective. Whenever powers act in various extents and headings, it is basic to know the moderate powers and preservation of energy. Here, moderate power is a power where the complete work done in any moving article between two unmistakable focuses is autonomous of the way taken. Though, the protection of energy expresses that the whole energy of any disconnected framework doesn’t change throughout time.

Kinetic Energy Examples

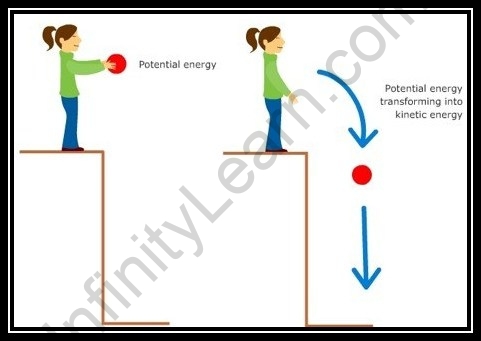
Remembering the above equation for dynamic energy, take a gander at a couple of the models seen in day-to-day existence circumstances.

1. A plane has tremendous motor energy in-flight on account of its quicker speed and colossal mass.
2. A baseball after it is tossed will have a lot of dynamic energy as a result of its high speed, and in spite of its more modest size and mass.
3. A declining skier descending from above will show colossal active energy due to its high speed and mass.
4. Before a golf ball has been struck shows no dynamic energy as its speed is zero.
5. At the point when a space rock falls at a staggering velocity, it has a tremendous measure of dynamic energy.
6. A vehicle going not too far off has less active energy when contrasted with that of a semi-truck on account of the less mass of the vehicle than the truck.

Kinetic Energy Units

Whenever we accept the unit of mass as a kilogram and speed as a meter for each sec, the active energy has the unit of kilograms per meter square for each Second Square. It is generally estimated in Joules. In this way, the SI unit of dynamic energy is Joule (J), which is unequivocally 1kg.m² .

Dimensional Formula of Kinetic Energy

The formula(dimensional) of Kinetic Energy is [M¹ L² T^-2]

Where,

• M = Mass
• L = Length
• T = Time

Derivation

Kinetic energy (K.E) = [Mass × Velocity²] × 2^-1 . . . . . (1)

The formula(dimensional) of Mass = [M¹ L⁰ T⁰] . . . . (2)

Since, Velocity = d/t = Distance × Time^-1 = [L] × [T]^-1

so, The formula(dimensional) of velocity = [M⁰ L¹ T^-1] . . . . (3)

On substituting (2) and (3) in (1) we get,

we know that, K.E(Kinetic energy) = [Mass .Velocity²] × 2^-1

So, K.E = [M¹ L² T^-2]

The representation(dimensional) of Kinetic Energy is [M¹ L² T^-2].

Significance of Dimension of Kinetic Energy in IIT JEE exam

It is critical to take a holistic approach to every facet of a subject’s chapter. It will not only adequately prepare you for the exam, but will also clarify your understanding of each topic. It will help you in JEE preparation and answer conceptual problems in the exam. The number of questions from the chapter unit and dimensions would be one or two, with a weightage of roughly four marks.