
Courses

By Shailendra Singh
|
Updated on 24 Jan 2025, 10:55 IST
Torque is the rotational equivalent of linear force in the realms of physics and mechanics. It describes the tendency of a force to cause or change the rotational motion of an object. Depending on the context, torque is also referred to as the moment, moment of force, rotational force, or turning effect. The concept of torque has its origins in Archimedes’ studies on levers, which demonstrated the principle of rotational force. Much like linear force propels an object in a straight line, torque is responsible for twisting or rotating an object about a specific axis.
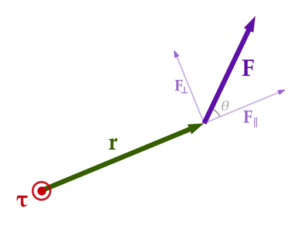
Torque (τ) is mathematically defined as the product of the magnitude of the applied force and the perpendicular distance from the axis of rotation to the line of action of the force. This distance is often referred to as the lever arm or moment arm. The formula for torque is:
τ = F ⋅ r ⋅ sin(θ)
Where:
Torque is essential in understanding rotational mechanics. Its effects can be seen in everyday actions such as opening a door, using a wrench to tighten a bolt, or spinning a wheel. The greater the force applied and the longer the lever arm, the greater the torque produced. For example:
This property highlights the importance of leverage in practical applications.
Torque is a vector quantity and has both magnitude and direction. The direction of torque is determined by the right-hand rule:

In a three-dimensional coordinate system, the torque vector is represented as the cross product of the position vector (r) and the force vector (F):
τ = r × F
The dimensions of torque provide a mathematical framework to understand its physical nature. Torque is calculated as:
τ = I ⋅ α
Where:
The moment of inertia is the rotational equivalent of mass in linear motion. It measures an object’s resistance to changes in its rotational motion and depends on the distribution of mass around the axis of rotation. The formula for the moment of inertia is:

I = k2 ⋅ m
Where:
The dimensional formula for the moment of inertia is:
[I] = M1 L2 T0
Angular acceleration represents the rate of change of angular velocity over time. It has the dimensional formula:
[α] = M0 L0 T-2
Substituting the dimensional formulas of moment of inertia and angular acceleration into the torque equation:
τ = [M1 L2 T0] ⋅ [M0 L0 T-2]
τ = [M1 L2 T-2]
Torque plays a vital role in various domains, including engineering, mechanics, and everyday life. Some notable applications include:
| Parameter | Formula | Unit | Dimensional Formula |
| Torque (τ) | F ⋅ r ⋅ sin(θ) | Nm | M L2 T-2 |
| Force (F) | m ⋅ a | N | M L T-2 |
| Lever Arm (r) | Distance from axis to force | m | L |
| Moment of Inertia | k2 ⋅ m | kg m2 | M L2 T0 |
| Angular Acceleration | Δω / Δt | rad/s2 | M0 L0 T-2 |
Torque is a cornerstone concept in rotational mechanics, bridging the gap between linear force and rotational motion. Its dimensional representation as [M L2 T-2] highlights its dependence on mass, distance, and time. From ancient levers studied by Archimedes to modern engineering marvels, torque remains pivotal in understanding and designing systems that rely on rotational dynamics.
The dimensional formula has been defined as the expression of a physical quantity in terms of its fundamental unit with appropriate dimensions.
Torque does have the dimension of force times distance, denoted by the symbol M L2 T-2. Even though the fundamental dimensions are the same as for energy or work, official SI literature recommends using newton metre (Nm) rather than joule.