
Courses

By Shailendra Singh
|
Updated on 23 Jan 2025, 11:54 IST
Question: A square of mass 2 kg put on a long frictionless even table is pulled on a level plane by a steady force F. It is found to move 10 m in the underlying two seconds. Track down the extent of F.
Answer:
We know that f=m.a,
From law of kinematics,
y-yo = ut + at2/2
10 = b22/2
b= 5m/s2
F=2*5 =10 N
Question: A vehicle moving at 40 km/h is to become by applying brakes in the following 4.0 m. On the off chance that the vehicle weighs 2000 kg, what normal power should be applied to it?

Answer:
u = 40km/hr = (100/a)m/s
According to law of kinetics,
0 = (100/1)2+ 2b.4
b= 15.432m/s2
F = 2000*15.432 = 3.086×104 N

Question: In a TV picture tube, electrons are jump-started out from the cathode with unessential speed and show up at a speed of 5 x 106 m/s in traveling one centimeter. Expecting straight-line development, find the consistent power applied on the electron. The heaviness of the (e)electron is 9.1 x 10-31 kg.
Answer:
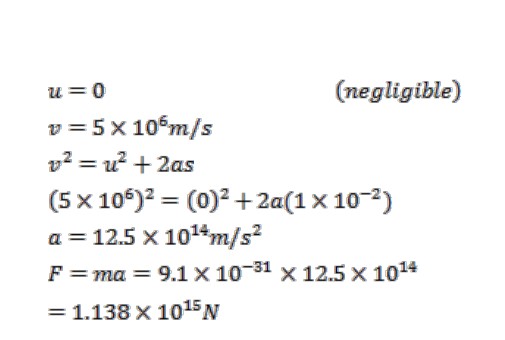
Question: A square of mass 0.2 kg is suspended from the roof by a light string. The second square of mass 0.3 kg is suspended from the initial square through another string. Track down the strains in the two strings. Take g = 10 m/s2 .
Answer:
A1 = 0.2g + A2
A2 = 0.3g = 3N
A1 = 0.2g + 3 = 5N
Question: Two squares of equivalent mass m are attached to one another through a light string. One of the squares is pulled along the line going along with them with a steady power F. Observe the strain in the string joining the squares.
Answer
F – T = ma
F = 2T
T = F/2
Question: A molecule of mass 50 g continues on a straight line. The variety of speed with time is displayed in the figure. Observe the power following up on the molecule at t = 2, 4, and 6 seconds.
Answer:
Given Slope of v-t graph provides acceleration, t=25, a= straight line(slope)
from t=0 to t=35= =5m/s2
t = 45, b = 0
t = 65, b = -5m/s2
F(t=25) = 0.25N
F(t=45) = 0N
F(t=65) = -0.25N
Question: Two squares An and B of mass mA and mB separately are stayed in touch on a frictionless table. The
experimenter pushes square A from behind with the goal that the squares speed up. Assuming square An applies a force F on square B, what is the power applied by the experimenter on A?
Answer: F’ = (ma + mb )g
Question : A molecule of mass 0.3 kg is exposed to a power F = – k x with k = 15 N/m. What will be its underlying speed increase assuming that it is set free from a point x = 20 cm?
Answer:
F = -kx = mb
b = -kx/m
= -10 m/s2
Question: Both the springs displayed in the figure are unstretched. Assuming the square is dislodged by a distance x and delivered, what will be the underlying speed increase?
Answer
-k1x – (k2x) =ma
a = -(k1 + k2)x/m
The section on Newton's Laws of Motion is clearly made sense of in HC Verma Class 11 Physics Part-1. The regulations and speculations are made sense of with the assistance of models and charts. The ideal way to gain this section from HC Verma, Physics Part-1 is by going through the clarifications, tests, and models completely. In the wake of learning the text appropriately, you should address the totals given in this book to evaluate your insight. Start with the model aggregates, and whenever you are done, contrast your answer and that given in the book.
Chapter 5 delves into Newton's three laws of motion, exploring concepts like inertia, force, and applications of these laws in various scenarios.
To master this chapter, thoroughly read the explanations, work through examples, and solve the exercises provided. Practicing problems enhances understanding and application skills.
Detailed solutions for Chapter 5 are available on educational platforms like Infinity Learn, offering step-by-step explanations to aid your comprehension.