Moment Of Inertia Of A Circle: In simple terms, this is the fundamental concept. It can be assumed that inertia is proportional to a body’s mass. When a body begins to rotate around a fixed axis, every element in the body travels in a loop with linear velocity, implying that each particle travels with angular acceleration. Yes, the proper definition of inertia is the tendency of a body to resist angular acceleration. It is the total mass of each particle in the body multiplied by the square of its distance from the axis of rotation.
Join Our Courses: JEE Class 11 Students | JEE Class 12 Students | JEE Dropper
Do you know how to calculate the moment of inertia of a circle? To understand this, we must first comprehend the derivation of a circle’s moment of inertia, which is discussed below. With this derivation, it will be easy to grasp how to get the moment of inertia of a circle.
According to the derivation of moment of inertia of a circle, the circular cross-section will be determined using the radius and an axis passing through the centre. This explanation will include the following steps:
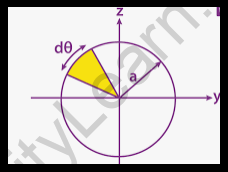
A moment of inertia is a quantitative measure of a body's rotational inertia—that is, the body's resistance to having its rotational speed modified by the application of torque—in physics (turning force).
The moment of inertia of a circle, also known as the second-moment area of a circle, is commonly calculated using the formula I = R4 / 4. The radius is R, and the axis passes through the centre. When we represent this equation in terms of the circle's diameter (D), it becomes I = D4 / 64.
The lift began abruptly. We take a step back. The satellite continues to move in a circular manner due to the inertia of motion. Even after you've stopped stirring, swirl the milk.
