
Courses

By Shailendra Singh
|
Updated on 21 Nov 2024, 16:14 IST
In analytic geometry, a hyperbola is formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are crossed. This intersection results in two unbounded curves that are mirror images of each other.
In other terms, a hyperbola is the locus of all points in a plane where the absolute difference between two fixed points on the plane remains constant.
The fixed points are the foci (single focus). The eccentricity of a hyperbola is the constant, and the directrix is the fixed-line. Eccentricity, denoted by the letter e, is a feature of the hyperbola that shows its lengthening.
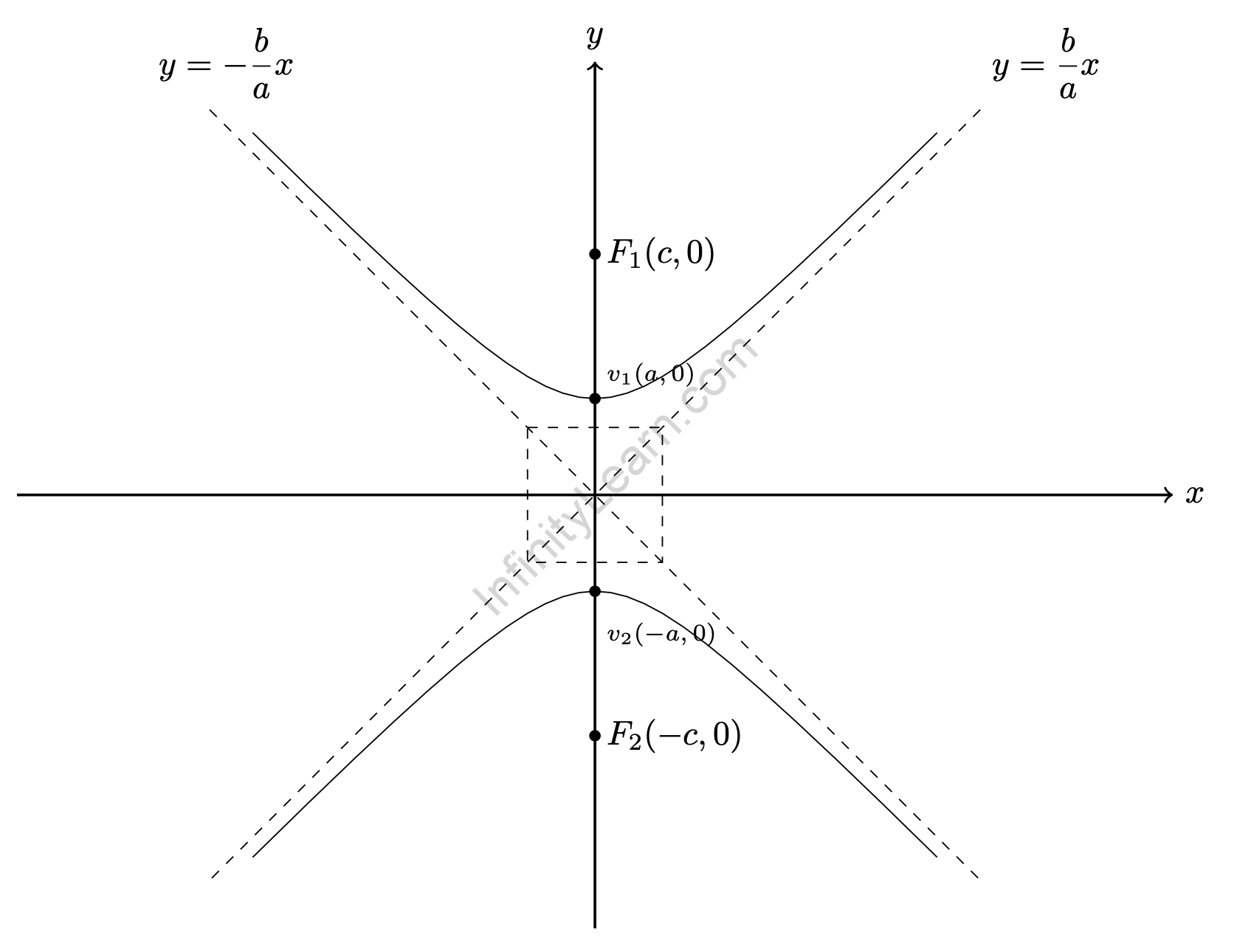
1. The Transverse Axis is a line that passes through the focus and is perpendicular to the directrix.
2. The vertices are the intersection points of the hyperbola’s primary axes.
3. The hyperbola’s Centre is the midpoint of its vertices.
4. The conjugate axis is a straight line that passes through the Centre of the hyperbola and is perpendicular to the transverse axis.

5. The Latus Rectum is a chord that runs through any of the two foci and is perpendicular to the transverse axis.
A vertical hyperbola is a shape that opens up and down. A horizontal hyperbola, also known as a sideways hyperbola, opens to the left and right. Each type of hyperbola has two symmetry axes.
The following are some of the most important properties of a hyperbola:
1. Every hyperbola has two foci or points of emphasis. At each point on the hyperbola, the difference in distances between the two foci is a constant.
2. The directrix is a straight line that connects both of the hyperbola’s foci and runs parallel to the hyperbola’s conjugate axis.
3. The directrix is always perpendicular to the transverse axis.

4. The transverse axis runs across the foci and vertices.
5. The tangent line of a hyperbola is always parallel to the directrix at its vertices.
6. For the hyperbola x²⁄a² – y²⁄b²= 1, the length of the latus rectum is 2b²⁄a.
7. If the transverse and longitudinal lengths are equal, a hyperbola is said to be rectangular or equilateral.
8. The difference in focal distances between any two points on the hyperbola is constant and equal to the transverse axis, i.e. ||PS – PS’|| = 2a. The focal length is measured by the distance SS’.
There are two standard Hyperbola equations.
The transverse and conjugate axes of each hyperbola are used to derive these equations. The typical hyperbola equation is x²⁄ a² – y²⁄ b² = 1, with the transverse axis as the x-axis and the conjugate axis as the y-axis.
Furthermore, another classic hyperbola equation is y²⁄ a² – x²⁄ b² = 1, with the transverse axis as the y-axis and the conjugate axis as the x-axis. The two conventional forms of hyperbola equations are shown in the graphic below.
Focus - The two fixed points that constitute the hyperbola are referred to as the focus and Foci, respectively. The middle of the line segment that connects the two foci is called the Centre. Or the place where the transverse and conjugate axes connect.
The asymptotes of the hyperbola are the tangents to the Centre. The line perpendicular to the transverse axis and passing through any of the foci parallel to the conjugate axis is known as the hyperbola's latus rectum. 2b²/a is the answer.