
Courses

By Shailendra Singh
|
Updated on 23 Jan 2025, 16:24 IST
A circle is a closed two-dimensional object in which all points in the plane are equidistant from a single point known as the “centre.” The line of reflection symmetry is formed by every line that travels through the circle. For any angle, it also exhibits rotational symmetry around the centre. In the plane, the circle formula is as follows:
(x-h)2 + (y-k)2 = r2
where (x,y) are the coordinate points
(h,k) is the coordinate of the centre of a circle
and r is the radius of a circle.
We know that Area is the space occupied by the circle.
Consider a concentric circle having an external circle radius to be ‘r.’ Open all the concentric circles to form a right-angled triangle. The outer circle would form a line having a length 2πr forming the base.
The height would be ‘r’
Therefore the area of the right-angled triangle formed would be equal to the area of a circle.
Area of a circle = Area of triangle = (1/2) ×b ×h
= (1/2) × 2π r × r

Therefore, the Area of a circle = πr2
The following are some of the most important basic features of circles:
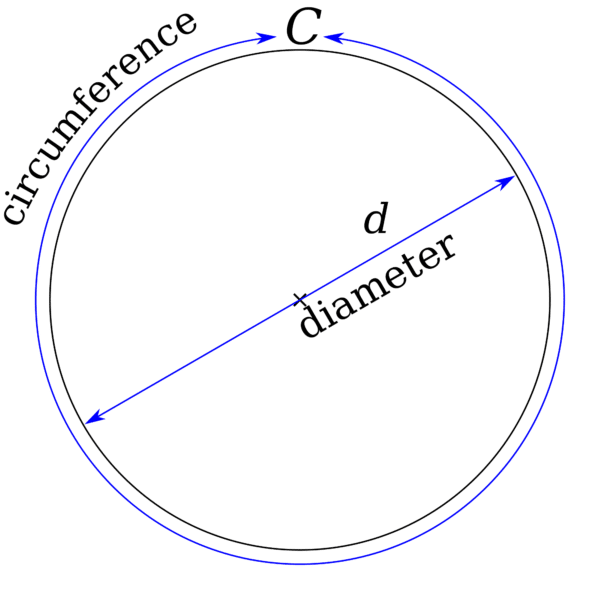
The radius of a circle is the line segment that connects the centre point and the circle surface. The diameter is considered the longest chord of a circle which is twice the radius.
The chord of a circle is defined as the straight line segment whose both endpoints touch the surface of a circle. The longest chord of a circle is a diameter.