
Courses

By Shailendra Singh
|
Updated on 18 Nov 2024, 18:36 IST
In general, kinematics is said to be the study of motion without regard for the forces that cause it. It basically means looking at how things move rather than why they move. It investigates the changes in values such as distance or displacement, speed or velocity, and acceleration over time. Kinematics could be studied in one dimension, such as a bus driving down a straight road, two dimensions, such as a canon being fired from the side, and even three dimensions.
As you add dimensions, things become a little more complicated. Kinematics is associated with many equations: equations for objects moving at a constant speed, equations for objects accelerating, and even complex equations for objects whose acceleration rate changes. However, it is sometimes easier to use graphical representations of kinematics quantities, or, in a nutshell, graphs.
Kinematics is the study in physics that generally defines motion with respect to time and space while ignoring the cause of that motion. The Kinematics equation is a set of equations that can derive an unknown aspect of the body’s motions if the other aspects are provided.
Kinematics, basically describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without taking into account the forces that cause them to move. Kinematics is often known as “geometry of motion” and is considered a branch of mathematics at times and the kinematics problem begins by describing the geometry of the system and announcing the initial conditions of any known values of point position, velocity, and/or acceleration within the system.
Geometry arguments can then be used to determine the position, velocity, and acceleration of any unknown parts of the system. Kinetics is the study of how forces act on bodies, not kinematics.
In astrophysics, kinematics is used to describe the motion of celestial bodies and collections of such bodies. Kinematics is a term used in mechanical engineering, robotics, and biomechanics to describe the motion of systems made up of joined parts (multi-link systems), such as an engine, a robotic arm, or the human skeleton.
Geometric transformations, as well known as rigid transformations, are used to describe the movement of components in a mechanical system, making it easier to derive the equations of motion. They are indeed important in dynamic analysis.
Kinematic analysis is indeed the measurement of the kinematic quantities used to describe motion. In engineering, for example, the kinematic analysis may be used to determine the range of movement for a given mechanism, followed by kinematic synthesis to design a mechanism with the desired range of motion. Moreover, kinematics studies the mechanical advantage of a mechanical system or mechanism using algebraic geometry.

The 4 kinematic equations that define the motion of an object are as follows:
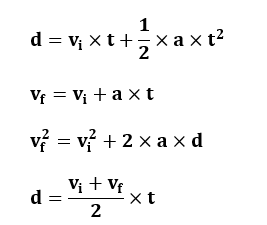
Here, d stands for the displacement of the object, t stands for the time for which the object moved, a stands for the acceleration of the object, v stands for the velocity of the object, indicates that the velocity value is the initial while indicates that the value of the velocity that is final.
In kinematics, three types of motion graphs are studied: displacement-time graphs, velocity-time graphs, and acceleration-time graphs.
The motion data of an object is plotted on an x-y grid, and a graph of the object’s motion is generated. Typically, the x-axis represents time, while the y-axis represents the object’s position, velocity, or acceleration.
The slope of the graph is velocity if the plot is position versus time. The slope of the graph is acceleration if the plot is velocity versus time. Jerk is the slope of acceleration versus time graph, but it is not a common concept covered in introductory kinematics.

To describe an object’s motion, you must first describe its position — where it is at any given time. More specifically, you must specify its location in relation to a convenient reference frame. The Earth is frequently used as a reference frame, and we frequently describe the position of objects in relation to their position to or from the Earth. The position of an object is generally represented mathematically by the variable x.
In order to define a position variable x, you must make one of two decisions. You must decide where x = 0 will be placed and which direction will be positive. This is known as selecting a coordinate system or selecting a frame of reference. Any frame is equally valid as long as you are consistent. You don’t want to switch coordinate systems in the middle of a calculation, though.
Consider yourself sitting on a train in a station when you suddenly notice that the station is moving backwards. Many people would say that they simply didn’t notice that the train was moving because it only appeared that the station was moving.
However, this demonstrates that there is a third arbitrary choice involved in selecting a coordinate system: valid frames of reference can differ from one another by moving relative to one another. It may appear strange to use a coordinate system that moves relative to the earth — but, for example, a frame of reference that moves along with a train may be far more convenient for describing what happens inside the train. When describing an object’s displacement, frames of reference are especially important.
Δx = xf – x0
Here, Δx is said to be displacement, xf is the final position, and x0 is the initial position.
A vector is described as any quantity that has both magnitude and direction, whereas a scalar only has magnitude. Distance is measured solely by magnitude, whereas displacement is defined by both direction and magnitude. One vector quantity is displacement, for example. A scalar quantity is something like distance.
A vector is really a geometric object with a magnitude (or length) and direction in mathematics, physics, and engineering that can be added to other vectors using vector algebra. In one-dimensional motion, the direction of a vector is simply indicated by a plus (+) or minus () sign. A vector has been frequently represented graphically as an arrow connecting an initial point A to a terminal point B, or as a line segment with a definite direction.
A few physical quantities, such as distance, have no or no specified direction. A scalar is a simple physical quantity in physics that is not affected by coordinate system rotations or translations. This is any quantity that has a magnitude but no direction and can be expressed by a single number.
Kinematic variables include distance, displacement, speed, velocity, acceleration, and jerk. Kinematics does not depend on an object's mass; it only describes an object's motion. This is entirely descriptive and based on their observations, such as throwing a ball or moving a train.
Kinematics has been used in astrophysics to describe the motion of celestial bodies and systems, as well as in mechanical engineering, robotics, and biomechanics to describe the motion of systems made up of joined parts.
Kinetics is concerned with determining the origin of various types of motions in an object, such as rotational motion in which the object experiences force or torque. Kinematics defines terms like acceleration, velocity, and object position.