
Courses

By Shailendra Singh
|
Updated on 4 Dec 2024, 12:17 IST
Sets: In mathematics, sets are collections of distinct objects forming a group. In a set have a group of items, days of the week, collection of numbers or members, types of vehicles etc. Every item or term in the set is called an element of the set. We generally set is denoted by {} curly bracket. Set can be expressed in roaster form or set builder form. let us discuss the type of set, properties, form of set and symbol of set.
It is a well-defined collection of objects. Sets are named and represented using a capital letter. In the set theory, the elements that a set comprises can be any kind of thing: people, letters of the alphabet, numbers, shapes, variables, etc. Let us take the example collection of even natural number less than 10 can be defined in a set but a collection of intelligent students in class can’t define.
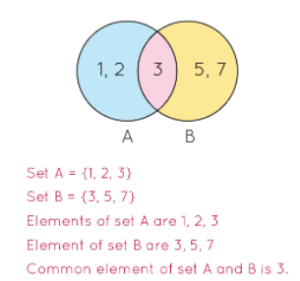
set of even natural number less than 10 (A) = {2,4,6,8}.
The items present in a set are called either elements or members of a set. All the elements of a set are enclosed in curly brackets also separated by commas. To denote that an element is contained or belong to a set, the symbol ‘∈’ is used. In the above example, 2 ∈ A. If an element is not contained in a set, then it is denoted using the symbol ‘∉’. Here, 3 ∉ A.
It is defined as the order of a set denoted by the total number of elements in the set. For natural even numbers less than 10, then we can define cardinality of set as n(A) = 4. One important condition to define a set is that all the elements of a set should be related to each other and share a common property. For example, if we define a set with the elements as the names of months in a year, then we can say that all the elements of the set are the months of the year.
Sets can represent in different ways. So the three important sets representation such as
Roaster form:- It is the most common or easier way of representing a set in roaster form in which the element is closed in curly brackets separated by commas. for example, Set B = {2,4,6,8,10}, which is the collection of the first five even numbers. if there is an endless list of elements in a set, then they are defined using a series of dots at the end of the last element If in the set have infinite represents as, U = {1, 2, 3, 4, 5 …}, where U is a set of natural numbers.
Set Builder form:- For represent the set in set-builder form has a certain rule that describes the common feature of the element of the set. If the set is represented in set-builder form then use of vertical bar sign in its representation, with a text describing the character of the element of the set. For example, A = { k | k is an even number, k ≤ 20}. The statement says, all the elements of set A are even numbers that are less than or equal to 20. Sometimes a “:” is used in the place of the “|”.

Semantic form:- The semantic notation describes a statement to show what are the elements of a set. Basically set describe in word form, For example, Set A is the list of the first five odd numbers.
Set can also be represented as Venn Diagram, it is a pictorial representation of sets, each set represents in the circle and each element of set represent inside the circles. If many sets are contained in a universal or big set then in that case rectangle enclose the subset which is represented as a circle. The Venn diagram represents such
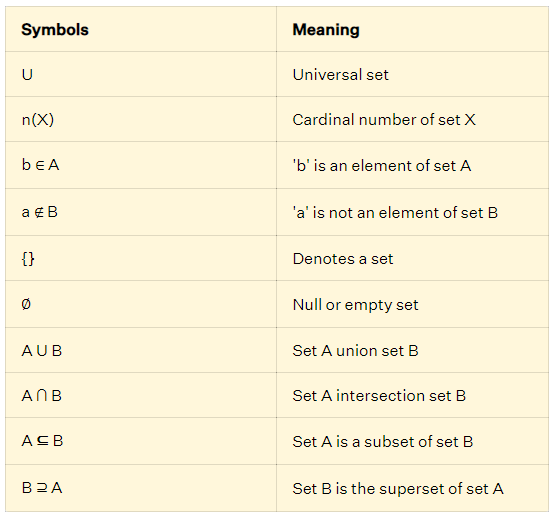
Set symbols are used to define the elements of a given set. The following table shows some of these symbols and their meaning.
Sets has different types such as singleton, finite, infinite, empty sets etc.

Singleton Sets:- It is that set in which have only one set is called singleton set or unit set. Example, Set A = { k | k is an integer between 3 and 5} which is A = {4}.
Finite set:- A set in which have finite or countable number of element is known as finite set. Exp., Set B = {k | k is a prime number less than 20}, which is B = {2,3,5,7,11,13,17,19}
Infinite Sets:- A set in which has an infinite number of elements is known as infinite set.
Example: Set C = {Multiples of 3}.
Empty Or null set:- A set that does not contain any element is called an empty set or a null set. An empty set is denoted as ‘∅’. It is read as ‘phi‘. Example: Set X = {}.
Equal Set:- If two sets have the same elements is known as equal set. Example: A = {1,2,3} and B = {1,2,3}. This can be represented as A = B
Disjoint Set:- Two sets are disjoint set if there are no common elements in both set. Example: A = {1,2,3,4} B = {5,6,7,8}. Here, set A and set B are disjoint sets.
Superset and Subset:- If every element of set A is set B, then set A is a subset of set B. It is denoted as A ⊆ B and B is the superset of set A. Example: A = {1,2,4} and B = {1,2,3,4}
Power set:- is the set of all subsets that a set could contain. Example: Set A = {1,2,3}. Power set of A is = {{∅}, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}.
Sets have different formula which is applied in algebra, statistics and probability.
For any two set A and B that are disjoint,
Properties
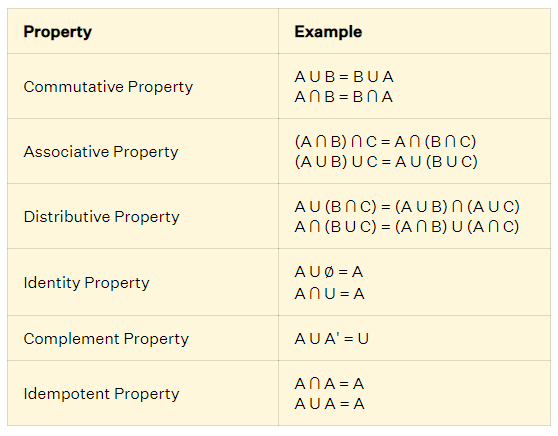
Similarly to numbers, sets have many properties such as.
Insets have some important operation which is useful for solving the problem such as
Union Sets:- Union of sets, which is denoted as A U B, lists the elements in set A and set B or the elements in both set A and set B. For example, {1, 3} ∪ {1, 4} = {1, 3, 4}
Intersection Sets:- The intersection of set which is denoted by A ∩ B lists the elements that are common to both set A and set B. For example, {1, 2} ∩ {2, 4} = {2}
Set difference:- Set difference which is denoted by A – B, lists the elements in set A that are not present in set B. For example, A = {2, 3, 4} and B = {4, 5, 6}. A – B = {2, 3}.
Set complement:- Set complement which is denoted by A’, is the set of all elements in the universal set that are not present in set A. In other words, A’ is denoted as U – A, which is the difference in the elements of the universal set and set A.
Cartesian Product of Sets:- The cartesian product of two sets which is denoted by A × B, is the product of two non-empty set, wherein ordered pairs of elements are obtained. For example, {1, 3} × {1, 3} = {(1, 1), (1, 3), (3, 1), (3, 3)}.
Types of sets depending upon elements present in the sets. So have different types of sets They are singleton sets, finite, infinite sets empty or null sets, equal sets, unequal sets, equivalent sets, overlapping sets, disjoint sets, subsets, supersets, power sets, and universal sets.
The union of two sets A and B are the elements from both set A and B, or both combined together. It is denoted using the symbol 'U'. For example, if set A = {1,2,3} and set B = {4,5,6}, then A U B = {1,2,3,4,5,6}. A U B is read as 'A union B'.