The magnitudes of coplanar, concurrent, and non-collinear forces that keep an object in static equilibrium are related by Lami’s theorem. The theorem seems to be extremely useful in analysing most mechanical and structural systems.
Lami’s Theorem asserts that “While three forces acting at a point are in equilibrium, then each force is proportional to the sine of the angle between the other two forces.” Now, consider three forces A, B, and C acting on a particle or rigid body at angles α, β and γ with each other.
It is written in mathematical or equation form as,
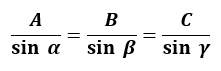
We can take FA, FB, and FC as the forces acting at a point. According to the statement of the theorem, we take the sum of all forces acting at a given point which will be zero.
That is, FA + FB + FC = 0
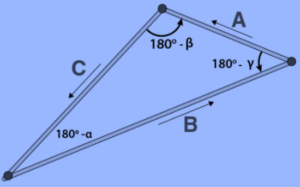
When a triangle is drawn, the angles formed by force vectors are,
Angles have been written in terms of complementary angles, and the triangle law of vector addition is used. Finally, by using the sine rule,
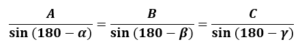
Then, we have,
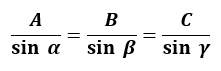
Thus, it is certainly seen that by applying the sine rule to complementary angles we arrive at the required result for Lami’s theorem.
The Sine Rule for triangles was used to derive this theorem. Once we represent the forces as lines, as in a free-body diagram, and translate them so that one head touches the tail of another, we can see that when there are three forces, if they are supposed to cancel each other out, they form a triangle.
They establish an open curve if they are not supposed to cancel each other. The Sine Rule applies only to triangles but not to all polygons. As a result, Lami’s Theorem only applies to three forces and not to ‘n’ forces.
Lami's theorem has been derived primarily from the Sine Rule for triangles. Whenever the forces are represented as lines, as in free-body diagrams, and translated in such a way that the head of one touches the tail of another, it is observed that when there are three forces, they cancel each other out, forming a triangle. When they do not cancel one another out, they will form an open curve. So because Sine Rule only applies to triangles, Lami's theorem only applies to three forces and not to any number of forces.
The magnitudes of concurrent, coplanar, and non-collinear forces that keep an object in static equilibrium have been related to Lami's Theorem. The Theorem would be extremely useful for analysing most mechanical and structural systems. The constant of proportionality is the same for all three forces.
