
Courses

By Shailendra Singh
|
Updated on 6 Dec 2024, 13:14 IST
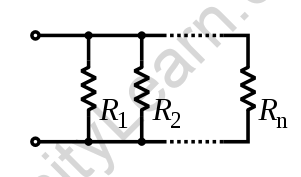
Parallel combinations of resistors: When several resistances are linked in such a way that one terminal of each resistance is connected at a common point A and the other terminals are connected at a common point B, and the potential difference across each resistor remains the same, this combination of resistances is known as a parallel combination of resistances. In a parallel configuration, three resistors R1, R2, and R are linked.
The same voltage difference V is maintained between the two terminals of the three resistors in this scenario. Because the resistors have various values, different amounts of current flow through them.
The circuit’s main current I separate into three portions at the junction a, then recombines at point b. Let’s call the currents running through the resistances R1 , R2, and R3 I1, I2, and I3, accordingly.
As a result, some parallel path currents I1, I2, and I3 are equivalent to the current I at the junction a.
As a result,
I = I1 + I2 + I3
Using Ohm’s law and the prospective difference between two terminals of V, we get

I1 is equal to V/R1; I2 = V/R2; I3 = V/R3
The equivalent resistance Rp can be stated as; if rather than three resistances, n numbers of resistances are placed in parallel.
1/RP is equal to 1/R1 + 1/R2 + 1/R3
When the voltage present across the resistors is the same, the circuit is said to be linked in parallel. The current is divided out and recombined when the branches intersect at a common point in such circuits.
In a parallel circuit, a resistor or any other component can be readily attached or disconnected without impacting the other elements.
Get the most Important Questions of Physics, Maths and Biology

A resistor is a two-terminal latent electrical part that goes about as a circuit component by executing electrical obstruction. Inside circuits, resistors lessen current stream and lower voltage levels. To restrict the section of charges in a circuit, most circuits utilize numerous resistors.
The two most fundamental resistor pairings are series and equal. We’ll discuss resistors in series and equal mixes in this article.
Transmitters (wire), a power source, a heap, a resistor, and a change make around a circuit. A circuit has a similar beginning and stops focus. Copper wire with no protection is normally involved as a channel. The gadget of switch that is utilized to open or close a circuit.
The progression of electrical flow in a circuit is constrained by resistors. A resistor is an uninvolved part, which suggests it simply consumes however not produces power. Demand in a circuit consumes electric energy by changing it over to light, heat, and different kinds of energy. A heap could be anything from a light source to a fan.
Distinct elements in electrical circuits are wired in series or parallel to create different resistive networking. Resistors can be connected in series or parallel and series across several loops in the same circuit to create a more complicated resistive network. Mixed resistor circuits are what all these circuits are titled.
Also at the end the total resistance must be known. Because resistors rarely exist in isolation, it’s critical to understand how to accomplish it. They’re typically part of a larger circuit with such a range of resistors coupled in multiple ways.
While the same current flow passes through the resistors, the circuit is said to be linked in series. The voltage across every resistor in such circuits varies.
If any resistor in a series connection is disrupted or a fault arises, the entire circuit is shut off. In contrast to a parallel connection, the design of a series circuit is simple.
Many circuits, as well as other configurations, can be evaluated as a blend of series and in parallel. The current which flows through each and every component in a series circuit will be the same, as well as the amount of voltage is the total of the individual potential drops over each component.
The voltage across each component in a parallel circuit is the same, and the total current is the total current flowing through each component.
RTotal = R1 + R2 +…… + Rn
The above mentioned equation is the total resistance in a series combination.
1/RTotal = 1/R1 + 1/R2 + …. + 1/Rn
Experienced teachers prepared Infinity Learn’s NCERT Solution for Physics. They make an effort to break down any topic into manageable chunks.
They began by discussing the main context of resistors and providing an explanation with examples. Then they went over all of the key questions and answers as students might easily answer on the NEET exam. Sentences are well-crafted, grammatically sound, and written in a straightforward manner.
There is also a fantastic possibility to clear any issue related to doubts with the infinity to learn the app. Experts are always on hand to assist students with their questions.
The expert or teacher puts forth their best effort on a regular basis to create their notes, and they ensure that all aspects are addressed thoroughly so that students receive the highest possible marks on their board exam.
Model question answers are described in detail with flawless clarification for each chapter to ensure that students understand the idea. Each math issue is resolved one at a time, with no step jumps, which is easy for kids to accept. Students taking board exams will benefit greatly from the elements listed above.
In a parallel combination, resistors are connected in such a way that the two ends of each resistor are connected to the same two points in the circuit. Essentially, the resistors share the same voltage across them but may have different currents flowing through them.
The equivalent resistance of resistors in parallel is always less than the resistance of the smallest resistor in the group. This is because parallel resistors offer multiple paths for current to flow, decreasing the overall resistance.
Yes, the formula for calculating the equivalent resistance works for any number of resistors in parallel. You simply take the reciprocal of the sum of the reciprocals of all resistances in the parallel combination.
In parallel, each resistor provides an additional path for current to flow, reducing the overall opposition to current flow. This is why the equivalent resistance of parallel resistors is lower than the smallest individual resistance.