
Courses

By Shailendra Singh
|
Updated on 16 May 2025, 12:52 IST
The determinant can always be of a square matrix. let A be a square matrix then we can express the determinant as det(A). it is a scalar quantity. Basically, determinant properties are used to find the value of the determinant with simple and least calculations. The properties of determinants basically depend on the row, the column and the element.
The determinant is used to solve the system of a linear equation and also used to find the inverse of a matrix.
Now let us discuss how to find the determinant of the 2×2 matrix and the 3×3 matrix. Let A be a square matrix, then the determinant of a matrix A can be represented as |A| or det(A).
Let A be a 2×2 square matrix.
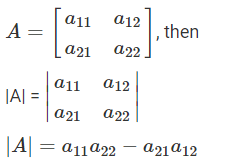
Let A be a 3×3 order square matrix.
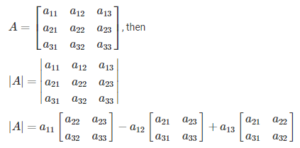

Here are the different properties of determinants:
the determinant value remains the same if the row and column are interchanged with each other. let us take an example of this
verify this Property for
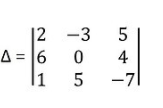
Let we will expand along the 1st Row
.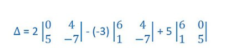

= 2[0(-7)-5(4)] + 3[6(-7) – 1(4)] +5[6(5) – 1(0)]
= 2(0 – 20) + 3(-42 – 4) + 5 (30 – 0)
= 2 (-20) + 3(-46) + 5(30)
= -40 – 138 + 150
= – 28
The sign of the determinant be change if any two rows and two column are interchanged each other. Sign of interchanged is ↔. It is also called as transpose property. Transpose of determinant can be expressed as
let us consider a determinant for this property.
verify this Property for
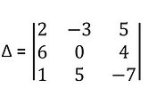
![]()
= 2[0(-7)-5(4)] + 3[6(-7) – 1(4)] +5[6(5) – 1(0)]
= 2(0 – 20) + 3(-42 – 4) + 5 (30 – 0)
= 2 (-20) + 3(-46) + 5(30)
= -40 – 138 + 150
= – 28
Now, interchange the element of Row -2nd and Row – 3rd
then, we get
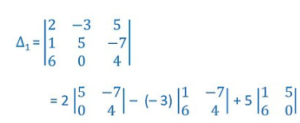
= 2 [5(4) – 0(- 7)] + 3[(14) – 6(-7)] + 5[1(0) – 6(5)]
= 2 (20 – 0) +3(4+42) +5 (0 – 30)
= 2(20) + 3(46) + 5(- 30)
= 40 + 138 – 150Δ¹
Δ¹ = 28
= – (- 28)
So, Δ¹ = – Δ
Hence, this property is verified.
we can say that if any two row or column are interchanged with each other then value of determinant changes.
Determinant value would be zero if any row or column in a square matrix are zero.
Let us take a example for this
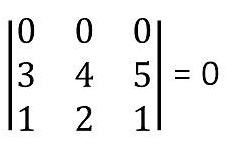
= 0
If we see any two-row or two columns of any determinant are identical, then the value of the determinant will be zero. Let us verify with the help of an example.
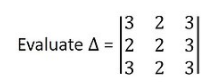
Let us expand this determinant
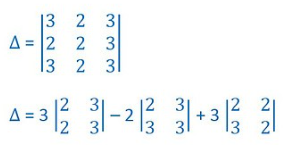
= 3[2(3) – 2(3)] – 2[2(3) – 3(3)] + 3[2(2) – 3(2)]
= 3(6 – 6) – 2(6 – 9) + 3(4 – 6)
0 + 6 – 6
= 0
Δ = 0
In this example 1st and 2nd row element are identical and determinant value get 0 after expanding.
if each element of a row or column is multiplied by any constant k, then, in that case, the determinant value will become k times. let us take an example of this.

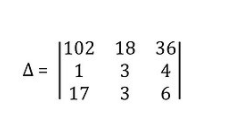
Here we can write, 102 = 6(17), 18 = 6(3), 36 = 6(6)

In the first row 6 is constant number
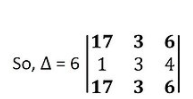
Elements of 1st row and 3rd row are same or identical
So, the value of the determinant is 0.
then, = 6 × (0)
= 0
Hence, Δ = 0
The determinant can be expressed as the sum of two or more determinants if the element of any row or column is expressed as the sum of the terms. Let us take an example of this
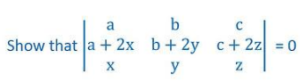
On solving the L.H.S
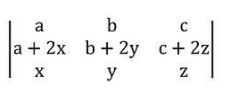
In the above determinant element of 2nd rows are the sum of two terms
So, we can write as
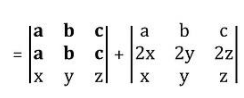
In the 1st determinant Row, 1st and Row 2nd are identical
we know that if any two-row or columns are identical, then the value of the determinant is 0.
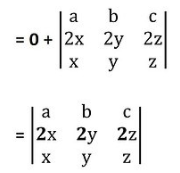
Also, each element of 2nd row are multiple of 2
then
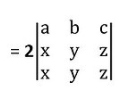
Row 2nd and Row 3rd are identical
= 2 × 0
= 0
= R.H.S
So, L.H.S = R.H.S
If in a determinant all the element just above or below the diagonal is zero then zero elements in that make a triangle. so it is called a triangular property. then the product of it gives a product of the diagonal element. So we can write this type of determinant as

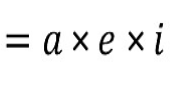
If each element of a row and column of a determinant is added with the equimultiples of the elements of another row or column of a determinant, then the value of the determinant remains unchanged. This can be expressed in the form of a formula as. ![]()
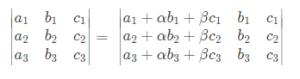
if a determinant Δ gives zero when we put x = α, then (x – α) is a factor of Δ.
Determinant of cofactor matrix:- we can write the determinant element as
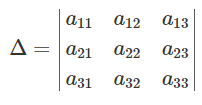
then
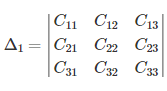
Q. find the determinant of the matrix using property?
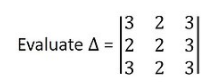
Let us expand this determinant
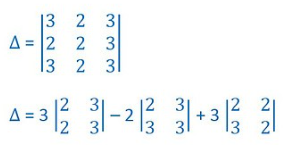
= 3[2(3) – 2(3)] – 2[2(3) – 3(3)] + 3[2(2) – 3(2)]
= 3(6 – 6) – 2(6 – 9) + 3(4 – 6)
0 + 6 – 6
= 0
Δ = 0
In this example 1st and 2nd row elements are identical and the determinant values get 0 after expanding.
The determinant is a scalar value that is associated with a square matrix. If A is a square matrix, then the determinant of this matrix is represented as | A| or det(A).