
Courses

By Shailendra Singh
|
Updated on 22 Nov 2024, 12:04 IST
A triangle is a polygon, it has three sides, three-angle and three vertices. triangle can be classified into the different type of triangle on the side and angles. we use properties of triangle to study detail about the triangle, but we also use them to compare two or more triangle. with the help of properties of triangle, we can determine equality and inequality of the triangle. let we will know about the properties of triangle.
Learn about the properties of triangles, we need to know about the types of triangles on which triangles’ properties depend. some properties are based on their side and angles and and some properties of triangle are common.
Types of triangle triangles are based on sides and angles.
with the help of properties we can identify the relationship between sides and angles of a triangles.
some important properties if triangle
If the sum of three interior angles of triangle is 180°.
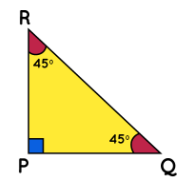
In the above figure, Let ΔPQR is a triangle.

then, ∠P+ ∠Q + ∠R = 180°
If the sum of the length of two sides of a triangle is greater than third side.
In the above figure we can see that ΔABC which show triangle inequality property.
If a = 5 unit, b = 7 unit,, c = 4 units, let we will will verify triangle inequality property as follow. 
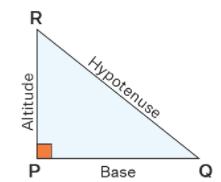
In the Pythagoras theorem, if in a right-angled triangle the square of the is equal to the sum of the square of other two sides.
we can write as

Hypotenuse² = Base² + Altitude².
or H² = B² + A²
If the side opposite the greater angle is longest side. let us consider a triangle ΔABC, in which ∠B is the greatest angle. So. AC is the longest side.
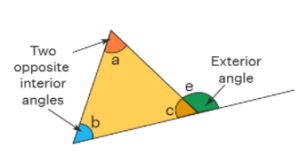
If the sum of the two opposite angle of triangle is equal to the exterior angle which is formed by extend the side of triangle.
Let ΔABC be triangle in which ∠E be the exterior angle.
So we can express such as
∠e = ∠a + ∠b
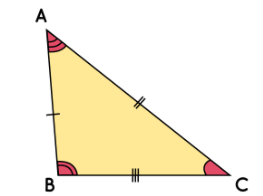
In the congruence property, two triangle are congruent if their corresponding sides and angles are equal.
they are 4 condition for two congruent triangle.
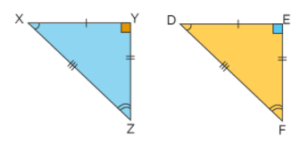
ΔXYZ ≅ DEFΔ because its hold all the congruency condition.
∠XYZ = ∠DEF
∠YXZ = ∠EDF
∠YZX = ∠EFD
XY = DE
XZ = DF
YZ = EF
A = ½ × b × h; where A is the area of triangle, ‘b’ is the base of the triangle and ‘h’ is the height of the triangle. unit of the area of triangle is square unit.
For finding the area of triangle, firstly we have to need the calculate the semi-perimeter(s)
we can express semi-perimeter as; S = a+b+c/2 .
Area of the triangle(A) = √s(s – a) (s – b) (s – c).
height can be defined as the measurement of an object in the vertical direction. Distance can be defined as measurement of an object in horizontal direction.
If we have to given area and base of a triangle ,then
h = 2A ÷ b
If we have to given area and height of a triangle,then
b = 2A ÷ h
2. By Pythagoras Theorem:- Pythagoras theorem is used in heights and distance to find the longest distance. it also define as the sum of the square of two side is equal to the square of third side.
i.e.; Hypotenuse² = Base² + Altitude²
or Altitude² = Hypotenuse² – Base²
or Base² = Hypotenuse² – Altitude²
3. Using trigonometry function:- Trigonometry is the study of relationship between sides angles of a triangle with the help of trigonometry function we can find the relationship between height and distance.
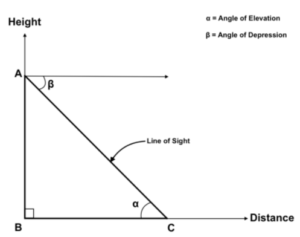
Many terms are associated with height and distance.
as shown in fig. line of sight, Angle of elevation and Angle of depression.
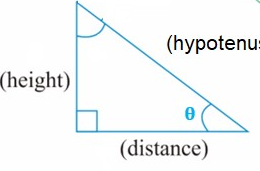
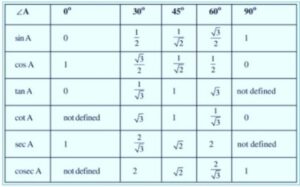
we can find height and distance relationship between and problems are solved by using using trigonometry ratio. we have 6 trigonometric ratio.
sinθ, cosθ, tanθ, cosecθ, secθ, cotθ
Let us consider a right-angled triangle

Some standard value of angles 0°, 30°, 45°, 60°, and 90° on we can find the value of height and distance.
let we do define a table for trigonometry ratios sine, cosine, cotangent, tangent, secant, and cosecant for above angles
Example:- Let an observer height is 1.5m is 28.5m away from a tree. The angle of elevation of the top of the tree is measuring 45. what is the height of the tree?
Solution:-
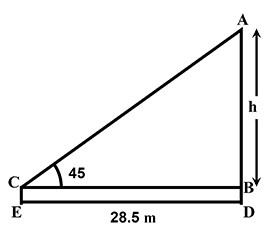
from the above fig.
BD = CE = 1.5m
In ΔABC,
∠B = 90°
⇒tanθ = P/B = AB/BC
⇒tan45° = AB/28.5
⇒ 1 = AB/28.5
⇒ AB = 28.5
Now, h = AB+BD = 28.5+1.5 = 30
So, the height of the tree is 30m
sum of all the sides of a triangle. Let ABC is a triangle in this triangle AB, BC and CA are side of triangle. then, perimeter of the triangle = AB + BC + CA
Semi-perimeter as (S) = a+b+c/2 . Area of the triangle(A) = √s(s - a) (s - b) (s - c)
Most commonly triangle is used to solve the problem of distance and height is a right-angled triangle.