A triangle formed 3 medians. In a triangle, the median is formed by joining a line segment at any vertex of the triangle and the mid-point of its opposite. It is also the line from the midpoint of a side to the opposite interior angle. the intersection of 3median is known as the centroid. Let us discuss the method for finding the median of a triangle, properties and example
A line segment joining a vertex to the mid-point of the side opposite to that vertex is called the median of a triangle. As shown in below fig., AD is the median, dividing BC into two equal parts, such that, BD = DC.
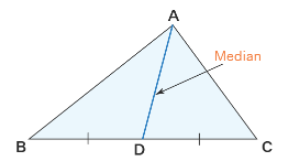
Length of a median can be found the different ways such as follows:
The formula for the length of the median to side BC =
ma =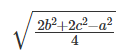 
In this a, b, c are the sides of the triangle and the length of the median from the vertex A is ma.
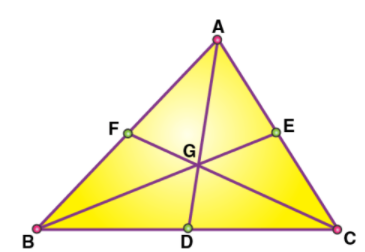
3 (AB2 + BC2 + CA2) = 4 (AD2 + BE2 + CF2).
Q. In the adjoining figure given, ∠PQR = 90∘ and QL is a median, PQ = 12cm, and QR = 16cm. Then, QL is equal to
Ans: Given that, PQ = 12 cm, QR = 16 cm and QL is a median.
∴ PL = LR …….(I)
In ΔPQR, (PR)2 = (PQ)2 + (QR)2 (By Pythagoras theorem)
= 144 + 256 = 400
⇒ PR = 20
Now, by theorem, if L is the mid-point of the hypotenuse PR of a right angled ΔPQR, then, we can write as:
QL = 1 / 2 [PR] = [1 / 2] * (20) = 10cm
The median of a triangle refers to a line segment joining a vertex of the triangle to the midpoint of the opposite side, thus bisecting that side. All triangles have exactly three medians, one from each vertex.
Median of a triangle was not always from a right angle. It will be formed is only in the case of an equilateral triangle in that case median is same as altitude.
