





Courses

By Shailendra Singh
|
Updated on 30 Dec 2024, 12:31 IST
The distance between two lines denotes how far apart the two lines are. A line is a figure formed when two points are connected with the shortest possible distance between them, and both ends of a line are extended to infinity. The perpendicular distance between two lines can be used to calculate their distance. In general, we calculate the distance between two parallel lines.
The distance between two straight lines in a plane is the shortest distance between any two points lying on the lines. We frequently deal with different sets of lines like parallel lines, intersecting lines, or skew lines when calculating.
The distance between two parallel lines is used to calculate how far apart the lines are. This can be accomplished by calculating the perpendicular distance between them. Using this approach, we can derive a formula and use it directly to find the shortest distance between two parallel lines. For two non-intersecting lines in the same plane, the distance between them is the shortest of all distances between two points on both lines.
Also Check: Distance Between Two Parallel Lines
The distance between two parallel lines is measured in millimetres, which is the perpendicular distance between any two points on a line.
The length of a line that intersects another line. Eventually, the shortest distance between such lines is zero.
For two skewed lines, the distance is equal to the length of the perpendicular between them.

Consider two parallel lines, which are represented as follows:
y = mx + c1 …(i)
y = mx + c2 ….(ii)
Where m = slope of the line
The formula can then be written as follows:
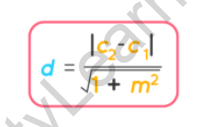

Check whether the given parallel line equations are in slope-intercept form (i.e. y= mx + c) or not.
In addition, if the equations of two lines are given in the slope-intercept form, the slope value should be the same for both lines.
Find the value of the interception point (c1 and c2) and the slope for both lines.
To calculate the value of y, substitute the values in the slope-intercept equation.
In conclusion, to find the distance between two lines, enter all of the values into the distance formula discussed below.
The length of the perpendicular between the two lines is equal to the shortest distance between skew lines.
The length of a line segment is the distance between two points. Congruent segments are segments that are the same length. By drawing a line with a ruler, we can calculate the distance between two points.
Yes, skew lines (non-parallel and non-intersecting lines in 3D space) have a shortest distance, calculated by finding the length of the perpendicular connecting the two lines.
The shortest distance between two lines is the minimum length of the perpendicular drawn between them, which can be calculated using vector geometry or algebraic formulas.