Important Topic of Physics: Conservative Forces

Introduction to Conservative Forces

When the force contains the property of the total work done in moving a particle between two points is independent of the path taken is called the conservative force. Similarly, if a particle travels in a closed loop then the total work done by a conservative force that is the sum of the force acting along the path multiplied by the displacement is zero.

The conservative force is dependent on the position of the object. If a force is conservative it is possible to assign a numerical value for the potential at any point. On the contrary, when an object moves from one location to another the force changes the potential energy of the object by an amount that is not dependent on the path taken and contributes to the mechanical energy and to the overall conservation of energy. Defining a scalar potential is not possible when the force is not conservative since taking different paths would lead to conflict in the potential differences between the start and endpoints.

Overview of Conservative Forces

One example of conservative force is the gravitational force whereas the frictional force is an example of a non-conservative force.

Some of the other examples of conservative forces are as follows:

• The force is present in an elastic spring.
• The electrostatic force is present in between two electric charges.
• The magnetic force is found between the two magnetic poles.

From the above-mentioned forces, the last two forces are also known as the central forces since they act along with the line joining the centers of two charged or magnetized bodies. The central force can be conservative only if it is spherically symmetric.

The conservative force can be defined as a force that is responsible to conserves mechanical energy. If there is a particle that starts at point A with a force F acting on it. Then the particle is moving around to the other forces and hence ends up at point A again. Since the particle may still move but at that instant when it passes point A again it has already traveled a closed path. If the net work done by force F at this point is 0, then F cleared the closed path test. Any forces which pass the closed path test for all possible closed paths are classified as the conservative force.

The example of conservative forces is as follows:

• The gravitational force
• The spring force
• The magnetic force
• The electric force

In the case of a non-conservative force, the mechanical energy which is lost and not conserved has to go somewhere else by the conservation of energy. Generally, the energy is turned into heat for example the heat generated by friction. Additionally to the heat sometimes the friction also produces some sound energy. The friction and air drag are classical examples of non-conservative forces. The water drag on a moving boat converts the mechanical energy of the boat into heat as well as in the sound energy. This also produces wave energy at the edges of its wake. These energy losses are irreversible due to the second law of thermodynamics.

A brief note of important concepts and laws

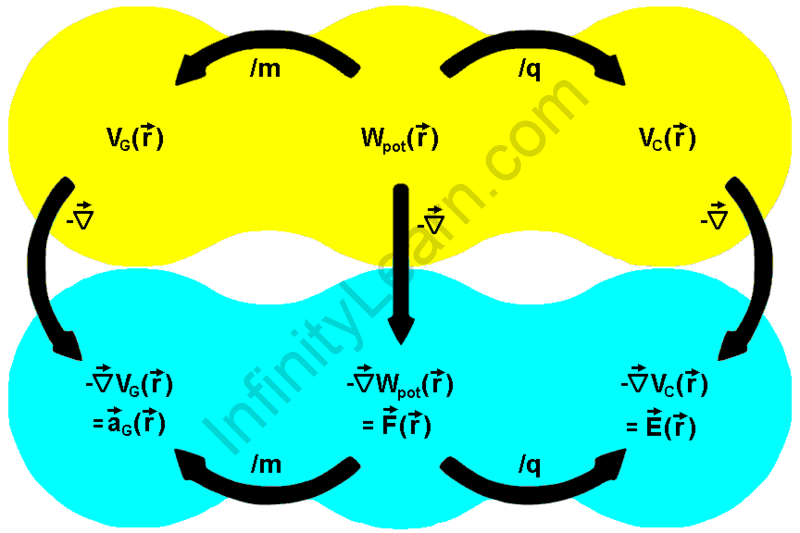
The term conservative force is initiated from the fact that when a conservative force exists it will conserve the mechanical energy. Gravitational force, electrical force, and spring force are the most familiar conservative forces.

The forces which are dependent on the velocity are not belonging to the force fields. In the magnetic force, the work done by a magnetic field on a charged particle is always zero but the force is not a vector field so it is not possible to evaluate its curl. Some of the authors classify the magnetic force as conservative whereas some do not consider it as a conservative force. In the magnetic force, many forces are depends on the velocity such as friction.

Since now we know what the conservative force is so let’s see some of its properties.

The properties are given as follows:

• During a loop, the work done by the conservative force will always be zero. This is due to there being no defined starting or ending point present inside a loop.
• One can easily reverse the work done when it comes to a conservative force. Hence the work done by the gravitational force can be easily reversed.
• And in the end, the conservative force only depends on the initial and final position of the object. Other all positions present in between do not affect the final result.