
Courses

By Shailendra Singh
|
Updated on 18 Nov 2024, 16:15 IST
Diffraction due to a single slit: Diffraction is a term that describes a variety of phenomena that emerge when a wave collides with an obstacle or an opening. It’s described as the bending of waves around the edges of an obstruction or through an aperture into the obstacle’s geometrical shadow region of the obstacle’s geometrical shadow. The diffracting object or aperture essentially becomes the propagating wave’s secondary source. When a single slit is exposed to monochromatic light. On a screen behind the slit, we see a diffraction pattern. Bright and dark bands can be seen in the diffraction pattern. The central band’s intensity is highest in the middle and gradually decreases on both sides.
The Huygens–Fresnel rule, which treats every spot in a propagating wavefront as just a group of discrete spherical wavelets, describes the diffraction phenomena. When a coherent source’s wave reaches a slit/aperture that is similar in size to its wavelength, as seen in the inserted image, the typical bending pattern is most pronounced. This is due to the inclusion, or interference, of various points on the wavefront that travel to the registering surface through routes of varying lengths. A complicated pattern of varied intensity can occur if there are several, closely spaced apertures.
When a light wave travels through a medium with a highly variable refractive index, or when a sound wave wanders through a medium with varying acoustic impedance, these effects occur as well – all waves, along with gravitational waves, water waves, as well as other electromagnetic waves like X-rays and radio waves, diffract. Quantum mechanics also indicates that matter has wave-like properties and, as a result, diffraction occurs.
According to the Huygens–Fresnel principle, a lengthy slit of microscopic width irradiated by light diffracts the light into a succession of circular waves, and the wavefront that emerges from the slit is a cylindrical wave of uniform intensity.
Interference effects occur in the space downstream of a slit that is broader than a wavelength. These can be explained by supposing the slit operates as if it contains a large number of point sources evenly spread across its width. When we examine light of a single wavelength, the evaluation of this system is simplified. These sources have the same phase if the incident light is coherent.
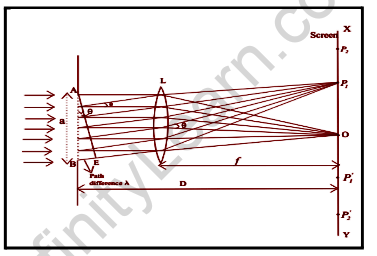
Light incident at a particular location in space downstream of the slit is composed of contributions from each of these point sources, and we should expect to detect minima and maxima in the diffracted light if the relative phases of these components vary by 2 or more. Discrepancies in the path lengths along which contributing rays approach the spot from the slit produce phase differences. The following reasoning can be used to determine the angle where a first minimum is achieved in diffracted light.
When the path difference between two sources is equal to λ/2, light from a source at the upper portion of the slit interferes destructively with light from a source in the center of the slit. Likewise, at the same angle, the source underneath the top of the slit will conflict destructively with the source just below the middle of the slit. We may apply this logic to the entire height of the slit and infer that the criterion for destructive interference again for the entire slit is the same as the requirement for destructive interference among two narrow slits separated by half the slit’s width.
The path difference is roughly d (sin θ)/2 so that the least intensity occurs at a certain angle θmin is given by

d sin θmin = λ
where
The light source and also the screen are both at limited distances from the slit in Fresnel diffraction. The incident waves aren’t in a straight line. Fraunhofer Diffraction occurs when the light source and the screen are both infinitely far away from the slit, resulting in parallel incident light rays.
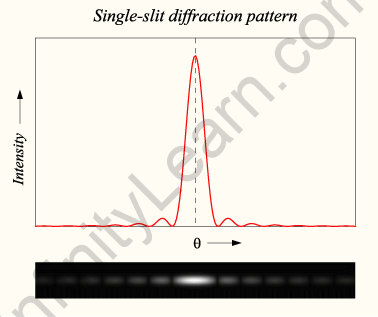
Sound waves’ diffraction is visible to us since wavelengths in the hearing region are roughly the same size as the things they meet, a condition that must be met if diffraction effects are to be easily noticed. Most materials need not diffract light appreciably since visible light wavelengths vary from around 390 to 770 nm. However, there are times when the apertures are tiny enough that light diffraction is visible. You can see a fairly good diffraction pattern consisting of light and dark lines running parallel to your fingers if you place your middle and index fingers close together look through the aperture at a light bulb.
Wave optics is an essential part of the NEET test as well as future reference and serious test planning. There are a couple of central issues in the Chapter that you can’t stand to disregard. A portion of the section’s key themes is light reflection, diffraction, single cut diffraction, the impedance of light, and light refraction. Inboard tests, inquiries from this section contain mathematical and definitional issues.

Using a mirror, we can shift the direction of light. To save energy, this easy technology is utilized to create light tunnels in newly constructed dwellings. A light tunnel collects sunlight and reflects it through a tunnel lined with mirrors at precise angles so that light is reflected inside the house at the other end.
For Fresnel diffraction, the light source and the screen are both finite distances from the slit, whereas, for Fraunhofer diffraction, the distances are limitless. For the latter, the incident light rays are parallel (plane wavefront). The incident light for Fresnel diffraction can be
The entire reflection of light rays inside the medium is known as total internal reflection.
The space either between 2 consecutive bright or dark fringes is known as fringe width.