A plane mirror and a concave mirror of curvature radius 60cm are placed facing each other, with a point object at the center of them. If the image formed by first reflection at the spherical and then at the plane mirror coincides with the object, then the separation between the two mirrors.

Let’s draw a simple sketch from the information given in the question for a better understanding.

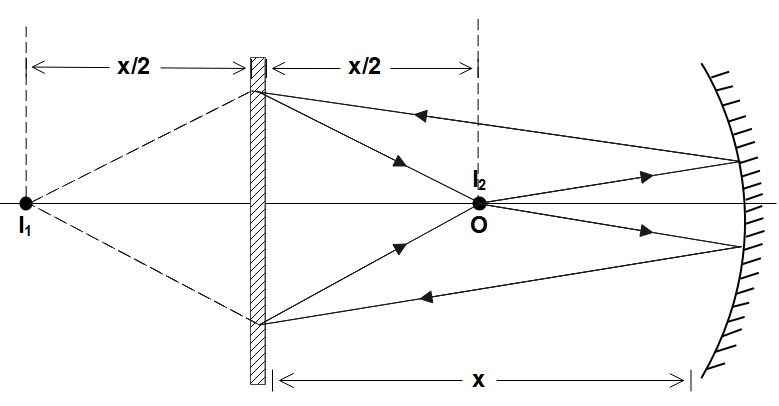
From the diagram, you should be able to understand that the incident rays from $O$ are reflected onto the plane mirror. This forms an image in the plane mirror, which we’ll be calling $I_1$. Now this image $I$₁ will act as the object for the plane mirror. So, its reflection forms an image $I_2$ again at $O$, as per the question. Let’s assume ‘$x$’ to be the distance between the mirrors and the object is placed at the center of them, say ${\displaystyle \frac{x}{2}}$.
Now, based on the diagram we can easily solve the question.
We have the mirror formula as,
${\displaystyle \frac{1}{f}}={\displaystyle \frac{1}{u}}+{\displaystyle \frac{1}{v}}$
Where,
$f$ is the focal distance
$u$ is the object distance
$v$ is the image distance
They’ve given the radius of curvature of the concave mirror as $60cm$, so the focal length is $f=-30cm$. The negative sign indicates that distances are measured from the pole, opposite to the direction of incident rays. Similarly, the object is placed at the center of two mirrors, so we have $u=-{\displaystyle \frac{x}{2}}$.
Substituting these values in the mirror equation, we have
$\begin{array}{rl} & {\displaystyle \frac{1}{f}}={\displaystyle \frac{1}{u}}+{\displaystyle \frac{1}{v}}\\ & \Rightarrow {\displaystyle \frac{1}{v}}={\displaystyle \frac{1}{f}}-{\displaystyle \frac{1}{u}}\\ & \Rightarrow {\displaystyle \frac{1}{v}}={\displaystyle \frac{1}{-30}}-{\displaystyle \frac{1}{-{\displaystyle \frac{x}{2}}}}\\ & \Rightarrow {\displaystyle \frac{1}{v}}={\displaystyle \frac{1}{-30}}+{\displaystyle \frac{2}{x}}\\ & \Rightarrow v={\displaystyle \frac{-30x}{x-60}}\end{array}$
The image $I_1$ is formed at this distance from the concave mirror. This image $I_1$ acts as an object for the plane mirror. Now, they’ve given in the question, that the plane mirror forms the image $I_2$ at $O$. From this, we need to understand that the object $I_1$ is at ${\displaystyle \frac{x}{2}}$ distance from the plane mirror as it forms its image $I_2$ at ${\displaystyle \frac{x}{2}}$ distance. So, the actual distance of $I_1$ from the concave mirror will be
Now the distance of $I_1$ from the concave mirror will be $x+{\displaystyle \frac{x}{2}}$.
Equating this to the result we’ve obtained,
$x+\frac{x}{2}=v$

$\Rightarrow x+\frac{x}{2}=\frac{30x}{x-60}$

$\Rightarrow \frac{3x}{2}=\frac{30x}{x-60}$

$\Rightarrow \frac{1}{2}=\frac{10}{x-60}$

$\Rightarrow x-60=20$

$\Rightarrow x=80cm$

Hence, option B is correct.