










Courses

By Maitree Choube
|
Updated on 27 Oct 2025, 11:52 IST
The Congruence of Triangles Class 7 Chapter 7 is an important part of the CBSE Class 7 Maths syllabus that helps students understand how two shapes or triangles can be exactly the same in size and shape. In this chapter, students learn the concept of congruence, different rules of congruence like SSS, SAS, ASA, RHS, and how to apply them to solve geometric problems.
Practicing extra questions on Congruence of Triangles Class 7 gives students a understanding of these rules and improves their logical thinking and problem-solving skills. These NCERT Solutions for Class 7 Congruence of Triangles are provided by Infinity Learn to prepare students for exams and higher classes. By solving these exercises and Class 7 maths extra questions regularly, learners can score better in exams and gain confidence in tackling complex Maths questions.
Questions on Congruence of triangles Class 7 is given below with answers. Students can practice these types of questions and clear their concepts.
Question 1. In the given figure, name (a) the side opposite to vertex A (b) the vertex opposite A to side AB (c) the angle opposite to side AC (d) the angle made by the sides CB and CA.
Solution: (a) The side opposite to vertex A is BC.
(b) The vertex opposite to side AB is C.
(c) The angle opposite to side AB is ∠ACB.

(d) The angle made by the sides CB and CA is ∠ACB.
Also Check: Rational Numbers Class 7 Extra Questions

JEE

NEET

Foundation JEE

Foundation NEET

CBSE
Question 2. Examine whether the given triangles are congruent or not.
Solution: Here, AB = DE = 3 cm BC = DF = 3.5 cm AC = EF = 4.5 cm ΔABC = ΔEDF (By SSS rule)
So, ΔABC and ΔEDF are congruent.

Question 3. In the given congruent triangles under ASA, find the value of x and y, ΔPQR = ΔSTU.
Solution: Given: ΔPQR = ΔSTU (By ASA rule) ∠Q = ∠T = 60° (given) \(\bar { QR }\) = \(\bar { TU }\) = 4 cm (given) ∠x = 30° (for ASA rule)
Now in ΔSTU, ∠S + ∠T + ∠U = 180° (Angle sum property) ∠y + 60° + ∠x = 180° ∠y + 60° + 30° = 180° ∠y + 90° = 180° ∠y = 180° – 90° = 90° Hence, x = 30° and y = 90°.
Question 4. In the following figure, show that ΔPSQ = ΔPSR.
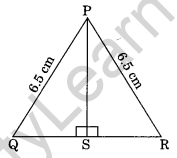
Solution: In ΔPSQ and ΔPSR,
PQ=PR=6.5cm (Given)
PS=PS (Common side)
∠PSQ=∠PSR=90° (Given)
So, both triangles have one right angle, one equal side, and an equal hypotenuse.
Hence, ΔPSQ ≅ ΔPSR by RHS rule.
Question 5. Can two equilateral triangles always be congruent? Give reasons.
Solution: No, any two equilateral triangles are not always congruent. Reason: Each angle of an equilateral triangle is 60° but their corresponding sides cannot always be the same.
Question 6. In the given figure, AP = BQ, PR = QS. Show that ΔAPS = ΔBQR
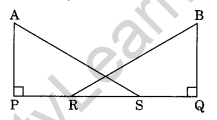
Solution: In ΔAPS and ΔBQR AP = BQ (Given) PR = QS (Given) PR + RS = QS + RS (Adding RS to both sides) PS = QR ∠APS = ∠BQR = 90° (Given) ΔAPS = ΔBQR (by SAS rule)
Question 7. Without drawing the figures of the triangles, write all six pairs of equal measures in each of the following pairs of congruent triangles.
(i) ΔABC = ADEF (ii) ΔXYZ = ΔMLN Solution: (i) Given: ΔABC = ΔDEF Here AB = DE BC = EF AC = DF ∠A = ∠D, ∠B = ∠E and ∠C = ∠F (ii) Given ΔXYZ = ΔMLN Here XY = ML YZ = LN XZ = MN ∠X = ∠M, ∠Y = ∠L and ∠Z = ∠N
Question 8. Lengths of two sides of an isosceles triangle are 5 cm and 8 cm, find the perimeter of the triangle. Solution: Since the lengths of any two sides of an isosceles triangle are equal, then
Case I: The three sides of the triangle are 5 cm, 5 cm and 8 cm. Perimeter of the triangle = 5 cm + 5 cm + 8 cm = 18 cm
Case II: The three sides of the triangle are 5 cm, 8 cm and 8 cm. Perimeter of the triangle = 5 cm + 8 cm + 8 cm = 21 cm Hence, the required perimeter is 18 cm or 21 cm.
Question 9. Write the rule of congruence in the following pairs of congruent triangles.
Solution: (i) Here, AB = ST = 3 cm BC = TU = 4.5 cm ∠ABC = ∠STU = 110° ΔABC = ΔSTU (By SAS rule) (ii) Here ∠PQR = ∠MNL = 90° hypt. PR = hypt. ML QR = NL = 3 cm ΔPQR = ΔMNL (By RHS rule)
Question 10. In the given figure, state the rule of congruence followed by congruent triangles LMN and ONM.
Solution: In ΔLMN and ΔONM LM = ON LN = OM MN = NM ΔLMN = ΔONM
Question 11. In the given figure, PQR is a triangle in which PQ = PR. QM and RN are the medians of the triangle. Prove that (i) ΔNQR = ΔMRQ (ii) QM = RN (iii) ΔPMQ = ΔPNR
Solution: ΔPQR is an isosceles triangle. [∵ PQ = PR] ⇒ \(\frac { 1 }{ 2 }\) PQ = \(\frac { 1 }{ 2 }\) PR ⇒ NQ = MR and PN = PM
(i) In ΔNQR and ΔMRQ NQ = MR (Half of equal sides) ∠NQR = ∠MRQ (Angles opposite to equal sides) QR = RQ (Common) ΔNQR = ΔMRQ (By SAS rule)
(ii) QM = RN (Congruent parts of congruent triangles)
(iii) In ΔPMQ and ΔPNR PN = PM (Half of equal sides) PR = PQ (Given) ∠P = ∠P (Common) ΔPMQ = ΔPNR (By SAS rule)
Question 12. In the given figure, PQ = CB, PA = CR, ∠P = ∠C. Is ΔQPR = ΔBCA? If yes, state the criterion of congruence.
Solution: Given: PQ = CB, PA = CR and ∠P = ∠C In ΔQPR and ΔBCA, PQ = CB (Given) ∠QPR = ∠BCA (Given) PA = CR (Given) PA + AR = CR + AR (Adding AR to both sides) or PR = CA ΔQPR = ΔBCA (By SAS rule)
Question 13. In the given figure, state whether ΔABC = ΔEOD or not. If yes, state the criterion of congruence.
Solution: In ΔABC and ΔEOD AB = OE ∠ABC = ∠EOD = 90° AC = ED ΔABC = ΔEOD Hence, ΔABC = ΔEOD RHS is the criterion of congruence.
Question 14. In the given figure, PQ || RS and PQ = RS. Prove that ΔPUQ = ΔSUR.
Solution: In ΔPUQ and ΔSUR PQ = SR = 4 cm ∠UPQ = ∠USR (Alternate interior angles) ∠PQU = ∠SRU (Alternate interior angles) ΔPUQ = ΔSUR (By ASA rule)
Question 15. In the given figure ΔBAC = ΔQRP by SAS criterion of congruence. Find the value of x and y.
Solution: Given: ΔBAC = ΔQRP (By SAS rule) So, BA = QR ⇒ 3x + 10 = 5y + 15 ……(i) ∠BAC = ∠QRP ⇒ 2x + 15° = 5x – 60° ……
(ii) From eq. (ii), we have 2x + 15 = 5x – 60 ⇒ 2x – 5x = -15 – 60 ⇒ -3x = -7 5 ⇒ x = 25 From eq. (i), we have 3x + 10 = 5y + 15 ⇒ 3 × 25 + 10 = 5y + 15 ⇒ 75 + 10 = 5y + 15 ⇒ 85 = 5y + 15 ⇒ 85 – 15 = 5y ⇒ 70 = 5y ⇒ y = 14 Hence, the required values of x and y are 25 and 14 respectively.
Question 16. Observe the figure and state the three pairs of equal parts in triangles ABC and DCB.
(i) Is ΔABC = ΔDCB? Why?
(ii) Is AB = DC? Why?
(iii) Is AC = DB? Why? (NCERT Exemplar)
Solution: (i) In ΔABC and ΔDCB ∠ABC = ∠DCB = 70° (40° + 30° = 70°) (Given) ∠ACB = ∠DCB = 30° (Given) BC = CB (Common) ΔABC = ΔDCB (By ASA rule) (ii) Yes, AB = DC (Congruent parts of congruent triangles) (iii) Yes, AC = DB (Congruent parts of congruent triangles)
Question 17. In the given figure, ΔQPS = ΔSRQ. Find each value. (a) x (b) ∠PQS (c) ∠PSR
Solution: (a) ΔQPS = ΔSRQ ∠QPS = ∠SRQ (Congruent part of congruent triangles) 106 = 2x + 12 ⇒ 106 – 12 = 2x ⇒ 94 = 2x ⇒ x = 47 ∠QRS = 2 × 47 + 12 = 94 + 12 = 106° So, PQRS is a parallelogram. ∠QSR = 180° – (42° + 106°) = 180° – 148° = 32°
(b) ∠PQS = 32° (alternate interior angles)
(c) ∠PSQ = 180° – (∠QPS + ∠PQS) = 180° – (106° + 32°) = 180° – 138° = 42° ∠PSR = 32° + 42° = 74°
Don't Miss Out: CBSE Class 7 Syllabus for All Subjects (2025-26)
| S. No. | CBSE Class 7 Syllabus 2025-26 |
| 1 | CBSE Class 7 Maths Syllabus |
| 2 | CBSE Class 7 English Syllabus |
| 3 | CBSE Class 7 Hindi Syllabus |
| 4 | CBSE Class 7 Science Syllabus |
| 5 | CBSE Class 7 Social Science Syllabus |
Question 18. In ΔABC, medians BD and CE are equal and intersect each other at O.
Prove that ΔABC is an isosceles triangle.
Solution: We know that the medians of a triangle intersect each other in the ratio 2 : 1.
So,
OB=OC and
OE=OD.
In ΔBOE and ΔCOD:
OB=OC
OE=OD
∠BOE = ∠COD (Vertically opposite angles)
So, ΔBOE ≅ ΔCOD (By SAS rule).
Hence, BE = CD and therefore AB = AC.
Thus, ΔABC is an isosceles triangle.
Question 19. Prove that the lengths of altitudes drawn to equal sides of an isosceles triangle are also equal.
(i) ∠TRQ = ∠SQR? (ii) If ∠TRQ = 30°, find the base angles of the ΔPQR. (iii) Is ΔPQR an equilateral triangle?
Solution: In ΔQTR and ΔRSQ ∠QTR = ∠RSQ = 90° (Given) ∠TQR = ∠SRQ (Base angle of an isosceles triangle) ∠QRT = ∠RQS (Remaining third angles) QR = QR (Common) ΔQTR = ΔRSQ (By ASA rule) QS = RT (Congruent parts of congruent triangles) Hence proved.
(i) ∠TRQ = ∠SQR (Congruent parts of congruent triangles)
(ii) In ΔQTR, ∠TRQ = 30° (Given) ∠QTR + ∠TQR + ∠QRT = 180° (Angle sum property) ⇒ 90° + ∠TQR + 30° = 180° ⇒ 120° + ∠TQR = 180° ⇒ ∠TQR = 180° – 120° = 60° ⇒ ∠TQR = ∠SRQ = 60° Each base angle = 60°
(iii) In ΔPQR, ∠P + ∠Q + ∠R = 180° (Angle sum property) ⇒ ∠P + 60° + 60° = 180° (From ii) ⇒ ∠P + 120° = 180° ⇒ ∠P = 180° – 120° = 60° Hence, ΔPQR is an equilateral triangle.
Also Check: Class 7 Maths Study Resource
No courses found
The Class 7 congruence of Triangles PDF includes questions based on SSS, SAS, ASA, and RHS congruence rules, helping students test their understanding of triangle properties and proofs.
You can download NCERT-based question banks and worksheets from Infinity Learn website that offer free Questions on Congruence Criteria in PDF format
The answers of such questions make students understand what sides and angles are equal and use the appropriate rules to prove the congruence of triangles in a fast and precise manner.
A Question Bank provides a variety of practice problems that gives an extra practice for students.
Extra questions encourage deeper thinking, improve problem-solving skills, and prepare students for higher-level geometry topics in CBSE and NCERT exams.