Important Topic: Matrices

Matrices are derived from matrices because matrices are the plural form of a matrix. It is a rectangular array that has m × n numbers or elements in the form of m horizontal lines called rows and n vertical lines are called columns. Two or more matrices can do different operations such as addition, scalar multiplication, multiplication, transposition, etc.

Let us describe the rule, properties, method for the solution of matrices, types of matrices and application of matrices.

Matrices:-

As we know that matrices are the plural form of a matrix. It is denoted by a double square bracket [ ]. A matrix is a rectangular array of numbers, variables, or expressions that are defined for operations like subtraction, addition and multiplications. the size of the matrix can be defined as m × n, where m is the row and n is the column. So can say that this order is the size of the matrix.

we can denote m × n order matrix such as

Method of calculating matrices:-

We can calculate or solve matrices by performing operations such as subtraction, addition, multiplication etc. calculation of matrices is depended upon a number of rows and columns.

• Addition of Matrices
• Subtraction of Matrices
• Scalar Multiplication
• Multiplication of Matrices
• Transpose of Matrices

Addition of matrices:-

addition of matrices depends upon a number of columns if the number of columns and rows of both the matrices are equal. At the time of adding 2 matrices, we add corresponding elements.

where i and j are the number of rows and the number of columns. For example:-

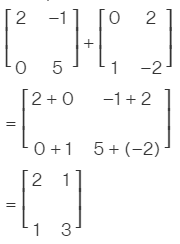
Subtraction of matrices:-

This operation is the same as addition, In this, we do only will do subtract the corresponding elements. For example

Scalar multiplication:-

The product of a matrix A with any number ‘c’ is obtained by multiplying every entry of the matrix A by c, is called scalar multiplication i.e.,

Properties of scalar multiplication in matrices:- The different properties of matrices for scalar multiplication of any scalars K and l, with matrices A and B are given

• K(A + B) = KA + KB
• (K + l)A = KA + IA
• (Kl)A = K(IA) = I(KA)
• (-K)A = -(KA) = K(-A)
• 1·A = A
• (-1)A = -A

Multiplication of matrices:-

Multiplication of matrices of any matrices is only can do if the number of columns in the first matrix and number of columns in the 2nd matrix is equal.

Properties of Matrix Multiplication:-

Properties of matrix multiplication are catrgroised in different properties. Let us take are A, B, and C three matrices:

• AB ≠ BA
• A(BC) = (AB)C
• A(B + C) = AB +AC
• (A + B)C = AC + BC
• 
• 

Transpose of Matrix:-

If in a matrix we replace the number of columns to the rows and the number of rows to the columns. Let us take an example for this of order 2 × 3, we have elements of the row in the matrix-1: 2, -3, -4, and row-2: -1, 7, -7. After transposing, we become the elements of row as-1: 2, -3, -4, and column-2: -1, 7, -7, which is shown in the below example:

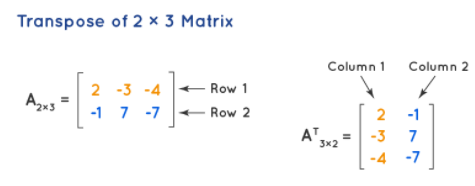
Trace of a Matrix:-

race of a matrix is defined as Tr(A) is defined as the sum of its diagonal elements. Some properties of trace of matrices are

• tr(AB) = tr(BA)
• tr(A) =
• tr (cA) = ctr(A), for scalar ‘c’
• tr(A + B) = Tr(A) + tr(B)

Determinant of Matrix:-

The determinant of the matrix is a scalar quantity. determinant of any matrix can be found if and only if it is a square matrix. determinant of any matrix expands along any row. Determinant of a Let A be any matrix determinant of this matrix is represented as |A|. let we want to find the determinant of the matrix A

then we can express it as

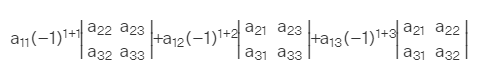
so this is the required formula for finding Determinant.

Minor of the matrix:-

It is a particular element. I is defined as the determinant of the matrix that is obtained when the row and column of the matrix in which that particular element lies are deleted, then minor of the element denoted by So for the given matrix, minor of of the matrix A

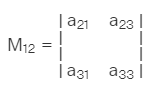
Similarly, can find all other minors of the matrix A, then we get minor matrix M of the given matrix A is:

Cofactors of Matrix:-

It is obtained when from matrix A when the minor is multiplied with (-1)^{i+j . Cofactor of any matrix is denoted as ${\mathrm{Cij\; .\; so\; we\; can\; write\; cofactor\; as:}}^{}$}

After finding the cofactor of the matrix, then we will get a cofactor matrix C of the matrix such as

Adjoint of Matrices:-

It can be found in the transpose of the cofactor matrix. So then get the adjoint of the matrix. Adjoint of matrices denoted as (Adj A).

The inverse of matrices:-

The inverse of any matrix is denoted as A^-1. If a given matrix is square then we can find the inverse of the matrix. The inverse of that matrix does not exist if the determinant of the matrix is |A| = 0. So the formula for the inverse of a matrix

A^-1 = (1/|A|)(Adj A)

Types of the matrix:-

The different types of the matrix can be defined as which is based on elements.

Row matrix:- If any matrix has a single row is called a row matrix.

Example: [1, −2, 4].

Column matrix:- If in a matrix having a single column is called a column matrix. Example: [−1, 2, 5].

Square matrix:- A matrix having an equal number of rows and columns is called a square matrix. for example

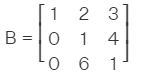
Rectangular Matrix:- A matrix having an unequal number of rows and columns is called rectangular matrix. for example

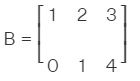
Diagonal matrices:- A matrix with all non-diagonal elements to be zeros is known as diagonal matrices. for example

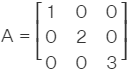
Identity matrices: It is that matrix in which diagonal elements equal to 1 is called an identity matrix. for example

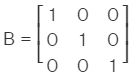
FAQ’s

How to solve matrix?

the matrix can be solved by performing operations on them like addition, subtraction, multiplication etc.

When the inverse of the matrix does not exist?

The inverse of any matrix will not exist If the determinant becomes zero.

What is the condition for matrix multiplication?

Let A and B be any matrix then if columns of matrix A equal to the of rows of the matrix B