Table of Contents
In motion, force has been described as an act that tends to maintain or alter a body’s motion or distort it. The idea and concept of force is commonly explained in terms of Isaac Newton’s three laws of motion, which are laid out in his Principia Mathematica (1687). So according to Newton’s first principle, a body that is at rest or moving at a uniform rate in a straight line will remain in that state until a force is applied to it. As per second law, when an external force acts on a body, the body accelerates (changes velocity) in the direction of the force. The magnitude of the acceleration seems to be proportional to the magnitude of the external force and inversely proportional to the mass of the body. As per Newton’s third law, when one body exerts a force on another, the second body exerts an equal force on the first. Such action-reaction principle describes why a force tends to deform (i.e., change the shape of) a body whether or not it causes the body to move. Whenever studying the motion of a body, it is common to overlook its deformation.
Overview
In fact, we can consider force as a vector quantity since it has both magnitude and direction. The use of vectors to represent forces implies that they are concentrated at a single point or along a single line. However, this is physically impossible. When applied to a loaded component of a structure, for example, the applied force generates an internal force, or stress, that is distributed across the component’s cross-section.
A charged particle can move in a circular or spiral path due to magnetic force. Cosmic rays are energetic charged particles in space that, in some cases, approach the Earth and Earth’s magnetic field could force these into spiral paths. Magnetic force keeps protons in giant accelerators moving in a circular path. This same curved paths of charged particles in magnetic fields underpin a wide range of phenomena and can even be used analytically, as in a mass spectrometer.
A force on an object or pull on an object is caused by its interaction with another object. If two objects interact, a force is exerted on each of the objects. A moving charge’s magnetic force is exerted in a direction perpendicular to the plane formed by its velocity and the direction of the surrounding magnetic field.
Force
Force is an impact in physics that can change the motion of an object. A force could indeed cause a mass object’s velocity to change (e.g., moving from a resting state), causing it to accelerate. In general, force could be described intuitively as a push or a pull. Since it has both magnitude and direction, a force is a vector quantity and it is measured in newtons, the SI unit of mass (N). The symbol F represents force (formerly P).
Newton’s second law, in its original form, asserts that the net force acting on an object is equal to the rate at which its momentum changes with time. If the object’s mass is constant, this law implies that an object’s acceleration;- is directly proportional to the total or net force acting on the object, is in the direction of the total or net force, and is inversely proportional to the object’s mass.
Thrust, which tends to increase an object’s velocity; drag, which decreases an object’s velocity; and torque, which produces changes in an object’s rotational speed, are all concepts related to force. Internal mechanical stress is the distribution of forces applied by each part of an extended body to the adjacent parts. The cause no acceleration of that body because the forces balance each other. Pressure, defined as the distribution of many small forces applied over a body’s surface, is a simple type of stress that, if unbalanced, can cause the body to accelerate. The deformation of solid materials or the flow of fluids is usually caused by stress.
Newton’s first law of motion dictates that unless acted upon by an external net force, objects continue to move at a constant velocity (resultant force). This law builds on Galileo’s discovery that constant velocity is associated with a lack of net force (see a more detailed description of this below). In place of the Aristotelian concept of the “natural state of rest,” Newton proposed that every object with mass has an innate inertia that functions as the fundamental equilibrium original or natural state. To put it differently, Newton’s empirical first law contradicts Aristotle’s intuitive belief that a net force is required to keep an object moving at a constant velocity.
As per Newton’s second law acceleration is directly proportional to force and inversely proportional to mass. Kinematic measurements can be used to define accelerations. However, while kinematics is well-described in advanced physics through reference frame analysis, there are still deep questions about what the proper definition of mass is. Although general relativity provides an equivalence between space-time and mass, it is unclear how or whether this connection is relevant on microscales in the absence of a coherent theory of quantum gravity. Newton’s second law can be taken as a quantitative definition of mass with some justification by writing the law as an equality; the relative units of force and mass are then fixed.
The application of symmetry to situations where forces can be attributed to the presence of different objects results in Newton’s Third Law. According to the third law, all forces are interactions between different bodies, and thus there is no such thing as a unidirectional force or a force that acts on only one body.
Force on a moving charge
One of the most fundamental known forces is the magnetic force on a moving charge. A magnetic force, attraction, or repulsion which develops between electrically charged particles as a result of their motion. It is the fundamental force responsible for effects such as the operation of electric motors and the attraction of magnets to iron. Between stationary electric charges, there are electric forces; between moving electric charges, there are both electric and magnetic forces. The magnetic force between two moving charges can be defined as the effect of one charge’s magnetic field on the other. Magnetic force is as significant as electrostatic or Coulomb force. However, the magnetic force is more complex than the relatively simple Coulomb force in terms of both the number of factors that affect it and its direction. Now, the magnitude of such magnetic force F acting on a charge q moving at v in a magnetic field of strength B is given by:
F = qvB sin θ
Here, θ is the angle formed by the directions v and B. Such a force is commonly referred to as the Lorentz force.
In fact, the magnetic field strength B is defined in terms of the force on a charged particle moving in a magnetic field. It is known that tesla (T) is the SI unit for magnetic field strength B, which is named after the eccentric but brilliant inventor Nikola Tesla (1856–1943). We solve F = qvB sin θ for B to see how the tesla relates to other SI units.
B=Fqvsinθ
We know that sin θ
is unitless, then the tesla will be:
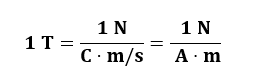
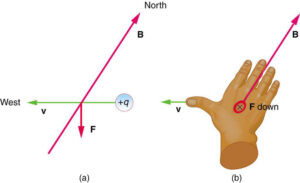
According to RHR-1, the magnetic force on a positive moving charge is determined by pointing the thumb of the right hand in the direction of v, the fingers are in the direction of B, and then a perpendicular to the palm in the direction of F. Another way to remember this is that there is only one velocity, which is represented by the thumb. Because there are many field lines, the fingers represent them. The force is directed in the same direction that you would push with your palm. The force on a negative charge is exactly opposite the force on a positive charge.
We could really make a few observations about magnetic force:
- The magnetic force seem to be perpendicular to the velocity and to the magnetic field (since it is given by their cross-product).
- The magnetic force’s direction is determined by the charge’s sign.
- Because the magnetic force is always perpendicular to the velocity, it can never do any work (and thus to displacement).
- If the particle’s velocity is in the same direction as the magnetic field vector, there is no force.
- The force raises as the magnetic field’s charge, speed, and strength increase.
FAQs
Does a moving charge experience a force?
The moving charge would always experience a force in the presence of a magnetic field. This force on the charged object is always perpendicular to the direction it is moving. Whereas magnetic forces cause charged particles to change direction, they do not change the particle's velocity.
Why force is applied on a moving charge in a magnetic field?
Current, or the flow of charge, is responsible for all magnetism. Magnetic fields apply a force on moving charges, and thus exert forces on other magnets with moving charges.
How does a charged particle move in magnetic field?
If indeed the field is in a vacuum, the magnetic field is the determining factor of motion. A charged particle in a magnetic field follows a curved path because the magnetic force is perpendicular to the direction of travel. This curved path is followed by the particle until it forms a complete circle.






