Table of Contents
Chapter 3, Rest and Motion Kinematics, manages the ideas of distance and relocation. Albeit both distance and uprooting indicate similar importance, they have a huge contrast. Distance is a scalar amount that signifies the region an individual or an article takes care of moving. Then again, dislodging is a vector amount, and it shows how far the article is situated from the objective.
Distance and relocation are communicated as d=d1+d2 and x= xf-xi,
where xf = last position and xi = starting position. If there should be an occurrence of removal, it is compulsory to determine the bearing of movement. Much like distance and uprooting, speed and speed additionally vary fundamentally. The speed of an article decides how rapidly an item moves. It is a scalar amount. Also, it is the rate at which an individual or an article covers distance. Normally, a quick individual or article covers a tremendous distance in a somewhat limited ability to focus accordingly has high velocity.
In actuality, speed can be characterized as the rate at which an item moving changes its situation. Deciding the bearing of the speed vector is straightforward. It is like the bearing in which it moves. In this way, the rate or speed of the article doesn’t make any difference when we think about its heading. Further, the section gives a brief look at speed increase.
The speed increase is likewise a vector amount and can be characterized as the rate at which an item moving changes its speed. In this manner, an item is supposed to be ‘speeding up’ on the off chance that it changes its speed at spans. Also, distance is determined utilizing the recipe s=ut+1/2(at2 ) . This condition is known as the second condition of movement. It is utilized to compute the distance(s) went by a body on schedule (t) with an underlying speed (u) and speed increase (a).
Question 1
A man needs to travel 50m due north, 40m due east and 20m due south to arrive at a field.
- What distance does he need to stroll to arrive at the field?
- What is his uprooting from his home to the field?
Answer 1
(a) Distance travelled = 50+40+20
=110m
(b) Displacement =50 ĵ +40 î- 20
=40î+30 ĵ
| disp |= √(40)2 + (30)2
=50m at an angle of Ɵ=tan-1(30/40 ) =37° north to east
Question 2
A molecule begins from the beginning comes the X-hub direct (20m, 0) and th32en returns along a similar line forthright (- 20m, 0). Track down the distance and dislodging of the molecule during the outing.
Answer 2
Distance voyaged = 20+40 =60m Displacement=20m in the negative course
Question 3
It is 260 km from Patna to Ranchi via air and 320 km by street. An aeroplane requires 30 minutes to go from Patna to Ranchi through a grand transport requires 8 hours
(a) Find the normal speed of the
(b) Find the normal speed of the
(c) Find the normal speed of the plane.
(d) Find the normal speed of the
Answer 3
(a) Vavg/plane = distance(d)/time(t) = 260/0.5 = 520kmph
(b) Vavg/bus = distance(d)/time(t) = 320/8 = 40kmph
(c) Vavg/plane = displacement/time(t) = 260/0.5 = 520kmph
(d) Vavg/bus = displacement/(t)time =260/8 = 32.5kmph
Question 4.
Whenever an individual leaves his home for touring by his vehicle, the meter peruses 12352 km. At the point when he gets back following two hours the perusing is 12416 km.
- What is the normal speed of the vehicle during the period?
- What is the normal speed?
Answer 4
(a) Vavg = total distance/time = (12416-12352)/2 = 32kmph
(b) Vavg = displacement/time = 0
Question 5
A competitor takes 2.0s to arrive at his most extreme speed of 18.0 km/h. What is the extent of his normal speed increase?
Answer 5
u=0; v=18*5/18 = 5m/s; t=2sec
v=u+at
5=0+a(2)
a=2.5m/s2
Question 6
The speed of a vehicle as a component of time is displayed in the given figure. Observe the distance went by the vehicle in 8 seconds and its speed increase.
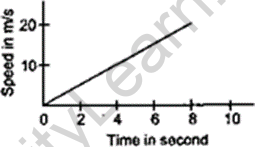
Answer 6
Acceleration=slope of (v-t) graph
a=tan θ = 20/8
=2.5m/s2
Distance=Area under (v-t) graph
= 8*20/2
=80m
Question 7
The speed increase of a truck began at t=0, fluctuates with time as displayed in the given figure. Track down the distance gone in 30 seconds and draw the position-time chart.
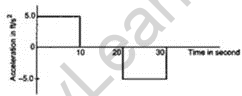
Answer 7
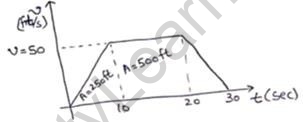
By velocity-time graph,
Acceleration =slope= v/t
5= v/10
V=50m/s
Distance=Area of v-t graph
= (30+10) (50)/2
=1000ft

Question 8
The given figure shows the chart of speed versus time for a molecule coming the X-hub.
Find
(a) The speed increase
(b) The distance went in 0 to 10s and
(c) The uprooting in 0 to 10s
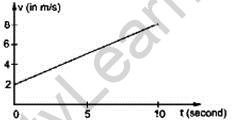
Answer 8
(a) Acceleration=slope of v-t graph
= 0.6m/s2
(b) Distance travelled = Area under v-t graph
= (2+8)10/2
=50m
(c) Displacement=50m

FAQs
What number of inquiries are there in the HC Verma Class 11 Physics part of Rest and Motion Kinematics?
There is an aggregate of 52 inquiries in the HC Verma Class 11 Physics part of Rest and Motion Kinematics. This multitude of inquiries is intended for a superior comprehension of Kinematics ideas and their applications. The majority of the inquiries have sub-parts that are interrelated. For instance, assuming there are three sub-parts in a specific inquiry, you can't address the subsequent sub-part without settling the first. This is the situation for a large portion of the inquiries in this activity, and there can be a couple of exemptions.
Are the HC Verma Class 11 Physics answers for the part of Rest and Motion Kinematics supportive for test planning?
Indeed, the HC Verma Class 11 Physics answers for the part on Rest and Motion Kinematics are extremely useful for test planning. The ideas that you create subsequent to gaining the ideas of Kinematics from the course reading are improved when you allude to these arrangements.





