Increasing And Decreasing Functions In Calculus

Introduction

Function: Allow us to think about x and y. Suppose a capacity from a set X to set Y is a task of set y to every one of the components of set X. Where x is an area and y is a co space.

Capacities might give a variable sort of data sources yet it gives a similar result which is remarkable to that specific capacity.

Definition:

An arranged arrangement of capacities that jelly or holds a specific request set is known as monotonic capacity. This study was first recorded by math and later it was added to an alternate hypothesis named request hypothesis.

Monotonic functions:

The capacity which we will talk about is expanding and diminishing capacities that go under the monotonic capacities.

So prior to moving to the theme, let us talk about what is known by monotonic capacities.

• Expanding and diminishing capacities can be effortlessly clarified with the assistance of subordinates as it is perhaps the main utilizations of subsidiaries.
• Subsidiaries are by and large used to distinguish whether the given capacity is expanding or diminishing at a specific time period.
• This increment and a decline of the capacity improve the propriety of the pace of progress of value got by the capacity.
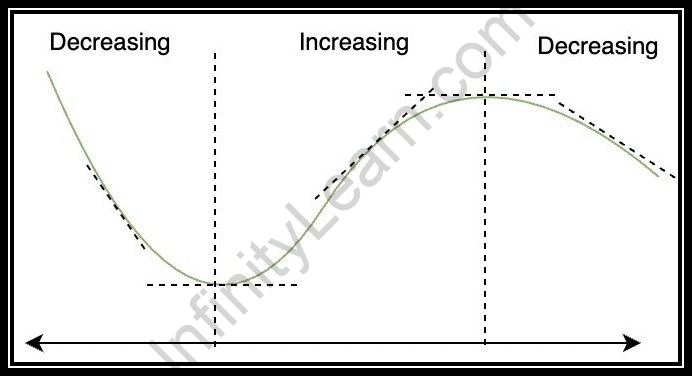
• The increment and decline of the capacity can be effectively clarified with the assistance of the accompanying chart as the name recommends, expansion in a capacity happens when the line of the diagram moves upwards while the lessening in a capacity happens when the line of the chart moves to descend, as in the accompanying diagram.
• On the off chance that we are moving from left to solidly in the above-shown diagram then, at that point, beginning from left the bend is moving downwards as the worth of y is diminishing and the worth of x is likewise diminishing at a given time period, so this is called a rising capacity.
• At the point when we move to the right half of the chart, the bend is expanding as both the upsides of x and y are expanding with the given time frame and known as the diminishing capacity.

Increasing and decreasing functions:

To comprehend expanding and diminishing capacities let us think about a straightforward model. It is viewed as there are different sides that are X and Y.

For a specific given work y=f(x),

• First case: assuming that the worth of the Y increments with the worth of the X, then, at that point, the condition is named as increasing function.
• Second case: assuming the worth of the Y diminishes with the worth of the x, then, at that point, the condition is named as in decreasing function.

Increasing Functions:

The function which is expanding at a given time period is called an increasing function.

• The capacity of y = f(x) includes a rising capacity having two places of stretches (x₁ and x₂ ) to such an extent that x₁ < x₂ with the practical disparity of f(x₁ ) ≤ f(x₂ ), then, at that point, the capacity can be supposed to be a rising capacity.
• In this imbalance, some piece of the rising capacity stays equivalent with both the capacities causing it to contrast from stringently expanding capacity.
• A stringently expanding capacity includes that work that doesn’t get equivalent to both the tomahawks in the middle of the rising system of the capacity at the given time frame.
• The stringently expanding capacity for the decent timespan having the time periods and x₂ can be expressed as f(x₁ ) < f(x₂ ).
• This expanding, too as stringently expanding capacities, can be effectively displayed on a chart with the assistance of the figures displayed beneath;

Decreasing Functions:

The function which is diminishing at the given timespan is called decreasing function.

• The capacity y = f(x) shows that the capacity has the span points of x₁ and x₂ through which a capacity can be diminishing or rigorously diminishing at the given time period.
• The capacity which is diminishing holds the novel disparity off(x₁ ) ≥ f(x₂ ).
• This disparity off(x₁) ≥ f(x₂ ) makes it one of a kind as the line of chart stays equivalent for both the tomahawks in a specific time span, making it unique in relation to stringently diminishing capacity.
• This rigorously diminishing capacity can be characterized as the capacity which stringently holds the imbalance and doesn’t have a similar incentive for both the tomahawks at a given time frame and shows the capacity as f(x₁) > f(x₂ ).
• The principle distinction between the rigorously endlessly diminishing capacity is that at any time period the capacity doesn’t continue as before in the stringently diminishing sort work.
• These diminishing sorts of capacity can be effectively clarified with the assistance of the diagram as displayed in the accompanying figures;

Steps involved in calculating the increase and decrease intervals:

• There are a few stages engaged with the most common way of tracking down the time frames and diminishing capacity, are as per the following:
• Initially, the given capacity is separated concerning the steady factor.
• Then, at that point, the primary subordinate is settled as a situation to offer the benefit of x for example if(x) = 0.
• In the wake of settling the condition of the primary subsidiary and the marks of irregularity, we get the open spans with the worth of x, through which the indication of the stretches can be thought about.
• The marks of the span framed are contrasted with track down the sign in their first subsidiaries. In the event that the indication of the stretch in their first subordinate structure gives more than 0, then, at that point, the capacity is supposed to be expanding in nature, while assuming the indication of the spans in their first subsidiary structure gives under 0, then, at that point, the capacity is supposed to be diminishing in nature.
• At long last, we get expanding as well as diminishing time periods work.
• There is a test through which the idea of the capacity can be recognized which is known as the principal subsidiary test. Through the primary subordinate test we can undoubtedly observe regardless of whether the capacity is monotonic in nature.

FAQs

Q: How do you have any idea that a capacity is increasing or decreasing?

Ans: To see if a capacity is expanding or decreasing, we need to recollect the accompanying two things:

• Allow us to assume that, work f(x) is differentiable and there exists an open span I, then, at that point, we can have
• On the off chance that F(x) is more prominent than and equivalent to 0, f is considered to increment in the span.
• On the off chance that f'(x) is not exactly or equivalent to 0, f is viewed as diminishing in the stretch

What is the significant distinction between expanding capacity and rigorously expanding capacity?

A chart can be named as expanding capacity Intergraph moves from left to right in some cases and at times it turns out to be level. However, on the off chance that the chart is continuously ascending from left to right just and it has no progressions then it is named as stringently expanding capacity.

What is the distinction between expanding and non-diminishing capacities?

In the event that a diagram is ascending from left to right and is generally more prominent than the other then it is named as expanding capacity. Then again assuming that one capacity is rarely more than the other or is generally not exactly the other then it is named as diminishing capacity.