Table of Contents
A rotating body’s kinetic energy can be compared to linear kinetic energy and described in terms of angular velocity. The total kinetic energy of the extended object is defined as the sum of the translational and rotational kinetic energies of the centre of mass. For a constant axis of rotation, the rotational kinetic energy is represented as follows. Rotational Kinetic Energy is the kinetic energy associated with an object’s rotational motion= 1/2 (mv2). Every particle in an object has the same angular speed, and tangential speed depends on the distance r from the axis of rotation. The total kinetic energy of a rotating object is the sum of the kinetic energy of all of the object’s individual particles.
Kinetic energy of rotation=(KR) = ∑ 1/2 (mv2) = 1/2 ∑ (m r2 ω2) = 1/2 (∑ m r2) ω2.
As a result, the Dimensional Formula of Rotational Kinetic Energy = M1L2T-2 and the SI unit of Rotational Kinetic Energy is the Joule (J).
Rotational Kinetic energy
Rotational energy is generated as a result of an object’s rotation and is a component of its total kinetic energy. When the rotational energy of an object is considered separately across its axis of rotation, the moment of inertia is observed. The definition of rotational energy, also known as angular kinetic energy, is as follows: The kinetic energy generated by an object’s rotation, which is a component of its total kinetic energy. The rotational kinetic energy is proportional to the rotational inertia and the square of the angular velocity magnitude. A rolling object has kinetic energy in both translational and rotational directions.
Rotational Kinetic Energy Formula
A rotating object’s rotational kinetic energy can be expressed as half of the product of the object’s angular velocity and moment of inertia around the axis of rotation.
Mathematically, this is written as:
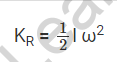
Where,
KR stands for Rotational Kinetic energy.
I represent the moment of inertia and is the angular velocity.
Parallel to the principle of work and energy, the expression can be designed for linear and rotational kinetic energy. Consider the specific parallel between a fixed exerted torque on a wheel with a moment of inertia and force on a mass m, both of which start from rest. According to Newton’s second law, acceleration equals resultant velocity divided by time, and average velocity equals half of the final velocity. The angular acceleration given to the wheel in the rotational case is derived from Newton’s second law of rotation. The torque of the rotation angle is the mechanical work required during rotation. For unattached objects, the axis of rotation revolves primarily around the centre of mass.
Frequently Asked Questions (FAQs)on Rotational Kinetic Energy
What has rotational kinetic energy?
Rotational kinetic energy is the energy possessed by an object due to its rotation around an axis. Anything that spins or rotates has this kind of energy.
What is the formula for rotational kinetic energy?
The formula for rotational kinetic energy is (1/2) * I * ω^2, where 'I' represents the moment of inertia of the object and 'ω' represents its angular velocity.
What does rotational kinetic energy depend on?
Rotational kinetic energy depends on the moment of inertia and the angular velocity of the object. The larger the moment of inertia or the faster the angular velocity, the higher the rotational kinetic energy.
What is the difference between kinetic energy and rotational kinetic energy?
Kinetic energy refers to the energy of an object due to its motion, generally in a straight line, while rotational kinetic energy refers to the energy due to its rotation around an axis.
Why is rotational kinetic energy important?
Rotational kinetic energy is important as it helps in understanding and analyzing the rotational motion of objects. It's crucial in many fields including engineering, physics, and astronomy.
What four factors affect rotational kinetic energy?
The four factors affecting rotational kinetic energy are the mass of the object, the shape of the object, the speed of rotation, and the axis of rotation.
What are the rotational kinetic energy units?
The units of rotational kinetic energy are the same as that of regular kinetic energy, which is Joules (J) in the International System of Units.
What is the difference between rotational and kinetic energy?
The difference between rotational and kinetic energy is the type of motion they are associated with. Kinetic energy is linked with linear motion, while rotational energy is associated with rotational motion around an axis.




