Table of Contents
When the charge is present in any form, an electric field is associated with each point in space. The magnitude and direction of the electric field are represented by the value of E, which is also known as electric field strength, electric field intensity, or simply the electric field. Knowing the value of the electric field at a point, without knowing what caused the field, is all that is required to predict what will happen to electric charges near that point.
Instead of viewing the electric force as a direct interaction between two electric charges separated by space, one charge is thought to be the source of an electric field that extends outward into the surrounding space, and the force exerted on a second charge in this space is thought to be a direct interaction between the electric field and the second charge.
The electric field strength E at any point can be defined as the electric or Coulomb, force F exerted per unit positive electric charge q at that point, or simply E = F/q. The resultant force is doubled if the second, or test, the charge is twice as large; however, their quotient, the measure of the electric field E, remains constant at any given point.
The strength of the electric field is determined by the source charge rather than the test charge. Strictly speaking, the introduction of a small test charge, which has its own electric field, modifies the existing field slightly.
The electric field can be thought of as the force per unit positive charge that would be exerted before the presence of the test charge disturbs the field. The force exerted on a negative charge is directed in the opposite direction as the force exerted on a positive charge.
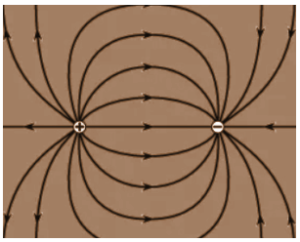
Because an electric field has both magnitude and direction, the force on a positive charge is arbitrarily chosen as the direction of the electric field. Because positive charges repel one another, the electric field surrounding a single positive charge is oriented radially outward. Electric fields are depicted as starting on positive charges and ending on negative charges when represented by lines of force or field lines.
A line that is perpendicular to a field line indicates the direction of the electric field at that point. The electric field is stronger where the field lines are close together than where they are separated.
Electric Field
The electric field is mathematically defined as a vector field associated with each point in space, the force per unit charge exerted on a positive test charge at rest at that point. The electric charge or time-varying magnetic fields generate the electric field. At the atomic level, the electric field is responsible for the attractive forces that hold the atomic nucleus and electrons together. A particle with electric charge q1 at position x1 exerts a force on a particle with charge q0 at position x0 of, according to Coulomb’s law. 
Where,
r1,0 is the unit vector pointing from point x1 to point x0. ε0 denotes the electric constant, which is also known as the absolute permittivity of free space is C2m-2N-1 When the charges q0 and q1 have the same sign, the force is positive and the direction is away from the other charges, implying that they repel each other. When the charges have opposite signs, the force is negative and the particles attract one another. The electric field is defined as the force per unit charge.

The electric field can be easily determined by applying Gauss’ law, which states that the total electric flux out of a closed surface equals the charge enclosed divided by the permittivity.
FAQs
Where is the electric field located?
The electric field radiates outward in all directions from the point charge. Spherical equipotential surfaces are represented by the circles. A vector sum of the individual fields can be used to calculate the electric field from any number of point charges.
What is an electric field, and what is its formula
The electric force per unit charge is another way to describe an electric field. The formula for the electric field is E = F /Q. Where E represents the electric field.




