Table of Contents
Complex numbers and their basic operations play an important role in the college algebra curriculum. The computation of roots and powers of complex numbers, as well as the solution of equations with complex roots, are common learning objectives in college algebra.
A portion of this instruction involves converting complex numbers to their polar forms and employing the work of the French mathematician Abraham De Moivre, known as De Moivre’s Theorem.
The goal of this research project is to investigate De Moivre’s Theorem, complex numbers, and the mathematical concepts and practises that lead to the theorem’s derivation. This document’s research section will include proof of De Moivre’s Theorem.
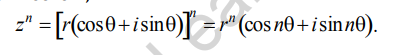
This theorem’s application, nth roots, and roots of unity, as well as related topics such as Euler’s Formula:
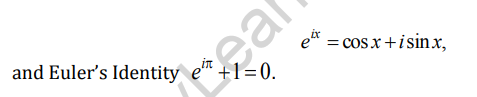
This study will provide a better understanding of the deeper mathematical concepts required to effectively teach the subject. Furthermore, it will give students the opportunity to investigate lessons and activities that will help them develop a greater appreciation for the significance and power of the complex number system.
DeMoivre’s Theorem, which connects complex numbers and trigonometry, is one of the most important and useful theorems in the field of complex numbers. It is also useful for determining relationships between trigonometric functions of different angles. DeMoivre’s Theorem, also known as “De Moivre’s Identity” and “De Moivre’s Formula,” is a mathematical theorem. The theorem is named after the great Mathematician De Moivre, who made numerous contributions to mathematics, primarily in the areas of probability theory and algebra.
The process of mathematical induction can be used to prove De Moivre’s theorem, which is a very important theorem in mathematics.
If the complex number z is equal to r(cos + I sin), then

Using mathematical induction, the preceding pattern can be extended to De Moivre’s theorem.
If n is a natural number and z = r(cos α + i sin α)
![]()
De Moivre’s Formula
Mathematical Statement: We have for any real number x
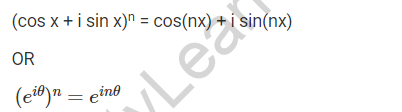
Where n is a positive integer, ” I ” denotes the imaginary part, and i = √(-1).
Assume i2 = -1. as well.
FAQs
What is the meaning of De Moivre's theorem?
The power of a complex number in polar form is equal to raising the modulus to the same power and multiplying the argument by the same power, according to De Moivre's Theorem. This theorem makes it simple to find the power and roots of complex numbers.
What is the use of de Moivre's theorem?
To find the roots of complex numbers, use de Moivre's formula. Abraham de Moivre (1667–1754) was a mathematician who pioneered the use of complex numbers in trigonometry.
Is de Moivre's formula applicable to negative integers n?
As a result, de Moivre's theorem holds true for n = 1. As a result, we have demonstrated that this is the case for negative integers. It is trivial to demonstrate the case where n = 0. As a result, we have demonstrated that de Moivre's theorem holds for all ? ∈ ℤ.




