Table of Contents
The partial derivative is used in vector calculus and differential geometry. The function in mathematics is sometimes dependent on two or more variables. Because the function is dependent on several variables, the derivative converts to the partial derivative. A partial derivative of a function with several variables is its derivative with respect to one of those variables while holding the others constant (as opposed to the total derivative, in which all variables are allowed to vary). In vector calculus and differential geometry, partial derivatives are used.
Assume we have a function f(x, y) that is dependent on two variables x and y that are independent of each other. The function f is said to be partially dependent on x and y. When we calculate the derivative of f, we get the partial derivative of f. When we differentiate the function f with respect to x, we take y as a constant, and when we differentiate f with respect to x, we take x as a constant.
The partial derivative of a function with respect to a variable x is denoted by a number of different terms.
with respect to a variable x is denoted by a number of different terms., , ,, , or.
The derivative of a function of several variables with respect to a change in only one of them in differential calculus. Partial derivatives can be used to analyse surfaces for maximum and minimum points, and they can also be used to generate partial differential equations. A first partial derivative, like an ordinary derivative, represents a rate of change or the slope of a tangent line. The slope of a three-dimensional surface is represented by two first partial derivatives, one in each of two perpendicular directions. The second, third, and higher partial derivatives reveal more about how the function changes at any point.
Partial Derivative Symbol
The partial derivative of any function with multiple variables is its derivative with respect to one of those variables while the others are held constant. The partial derivative of a function f with respect to a variable x is denoted by f’x,fx, ∂xf or ∂f/∂x. The partial derivative symbol ∂ is shown here.
Partial Derivative Formula
If f(x,y) is a function that partially depends on x and y, and we differentiate f with respect to x and y, the derivatives are referred to as the partial derivatives of f. The partial derivative of f with respect to x with y as a constant is given by;
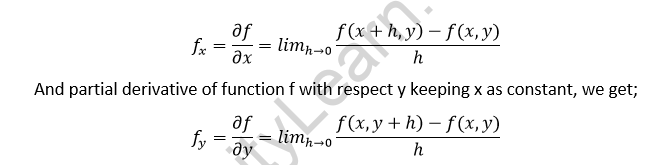
FAQs
What does a function's partial derivative represent?
A first partial derivative, like an ordinary derivative, represents a rate of change or the slope of a tangent line. The slope of a three-dimensional surface is represented by two first partial derivatives, one in each of two perpendicular directions.
What exactly are partial derivatives?
A partial derivative is defined as a derivative in which some variables are held constant while determining the derivative of a function with respect to the other variable.
How does one distinguish a multivariable function?
The first is the direct second-order derivative. In this case, the multivariate function is differentiated only once, with respect to an independent variable, while all other variables are held constant. The result is then differentiated a second time, this time with regard to the same independent variable.
