Table of Contents

Wave motion is the transfer of energy and momentum from one point in a medium to another without the actual transport of matter between two points. Wave motion has been classified into three types, which are as follows:
- The propagation medium,
- The dimensions wherein energy is propagated by a wave,
- The transfer of energy
Particles in a wave can move perpendicular to the wave direction (transverse) or parallel to it (parallel) (longitudinal).
Characteristics of Wave Motion
- The disturbance in wave motion travels through the medium as a result of repeated periodic oscillations of the medium’s particles about their mean position (or) equilibrium position.
- Without any actual transfer of medium particles, energy and momentum are transferred from one point to another.
- Since each particle receives disturbance slightly later than the particle before it, there is a regular phase difference between the particles of the medium.
- The velocity by which a wave is moving differs from the velocity with which particles vibrate about their mean (or) equilibrium position.
- The velocity of the wave motion continues to remain constant for a given medium, whereas the particle velocity changes continuously during its vibration about its equilibrium position.
- The particle’s velocity is greatest at the mean position and zeroes at the extreme position.
Waves on a String
Consider yourself to be holding one end of a string while the other end is secured and the string is pulled taut. After all, only when you flick the string either up or down. The wave which results from this motion is known as a transverse wave. A transverse wave is one in which the movement of the particles in the medium is perpendicular to the direction of the wave’s propagation. The rope serves as the medium through which the waves propagate in this case. While the rope moved up and down, the wave moved from one end to the other.
Speed of a Wave on a String
The velocity has been calculated by dividing the distance travelled by the time required to complete that distance. This one is found in waves by dividing the wavelength by the period:
V = λ/T
We could use inverse proportionality to period and frequency to solve this problem:
v = λf
Speed of a Wave on a Vibrating String
Waves on vibrating strings, including those found in musical instruments, are another example of waves on strings. Vibrating strings have been used by both pianos and guitars to produce music. In such cases, the frequency is what distinguishes the pitch and thus the note. The speed of a wave towards this type of string is proportional to the square root of the string’s tension and inversely proportional to the square root of the string’s linear density.
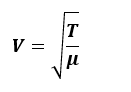
Reflections
Transverse waves in strings have been reflected when they meet one end, and interference occurs when the incident wave meets the reflected wave.
FAQs
What causes wave motion?
Wind is by far the most common cause of waves. Wind-driven waves, as well known as surface waves, are caused by the friction of wind and surface water. Once the wind blows across the surface of the ocean or a lake, the resulting disturbance produces a wave crest.
What is the top of the wave called?
The greatest possible part of a wave's surface is known as the crest, and the lowest part is known as the trough. The wave height is indeed the vertical distance between the crest and the trough.








