Continuity and Differentiability

Table of Contents

Introduction: Continuity and Differentiability – JEE

Continuity of a function is indeed a property of a function that results in the graphical representation of that function being a continuous wave. A differentiable function is something that has a derivative at every point in its domain.

Continuity

One of the most important things that require continuity is our families. Families are the basic unit of society. They provide us with our sense of identity and help us to learn the important values that we need to succeed in life. Families also provide us with a sense of continuity. They are a constant in our lives, no matter what else may change.

Another thing that requires continuity is our government. Our government is responsible for ensuring our safety and well-being. It provides us with essential services, such as education and healthcare. It also ensures that our economy is stable and that our laws are enforced. Our government is a vital part of our society and it requires continuity in order to function properly.

Finally, our economy requires continuity in order to thrive. Our economy is based on the principle of supply and demand. When there is a disruption in the supply or demand for a product or service, the economy suffers. This can lead to mass unemployment and economic recession. It is therefore essential that the economy maintain continuity in order to function properly.

In a world where change is constant, it is important to maintain continuity. Without continuity, there would be chaos. There are many things in life that require continuity in order to function properly. Families, governments, and economies are just a few of the important things that require continuity. If we want our families, governments, and economies to thrive, we must ensure that continuity is maintained.

Various aspects of nature exhibit the property of continuity. The rivers’ water flow is continuous. The passage of time in human life is continuous, implying that you are growing older all the time. And so forth. Correspondingly, in mathematics, we have the concept of function continuity.

If the succeeding three conditions are met, a function f(x) is said to be continuous at a point x = a, in its domain:

f(a) exists (i.e. the value of f(a) is finite)
Lim_x→af(x) exists (i.e. the right-hand limit = left-hand limit, and both are finite)
Lim_x→af(x) = f(a)

If indeed the three conditions mentioned above are satisfied for every point in interval I, the function f(x) is said to be continuous in the interval I = [x₁,x₂].

Even so, at the interval I’s endpoints, we don’t need to consider both the right-hand and left-hand limits when calculating Lim_x→a f(x).

For a = x₁, only the right-hand limit is required, and for a = x₂, only the left-hand limit is required.

Differentiability

If the derivative of the function f ‘(a) persists at every point in its given domain, the function f(x) is said to be differentiable at the point x = a.

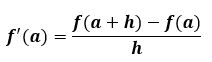
If a function seems to be continuous at one point, it is said to be differentiable at any point x = an in its domain. That’s not always true in the other direction.

A differentiable function’s graph demonstrates a non-vertical tangent line at each interior point in its domain. A differentiable function seems to be smooth (it can be approximated locally as a linear function at each interior point) and lacks any break, angle, or cusp.

Only when f is differentiable at point x₀, it must also be continuous at that point. Each and every differentiable function, in specific, must be continuous at all points in its domain. The converse is not true: a continuous function does not have to be differentiable. A function with a bend, cusp, or vertical tangent, for example, maybe continuous but not differentiable at the location of the anomaly.

Many functions encountered in practice have derivatives at all or nearly all points. Even so, according to Stefan Banach’s result, the set of functions with a derivative at some point is a small set in the space of all continuous functions. This means that differentiable functions are very unusual among continuous functions. The Weierstrass function will be the first known example of a function that is continuous everywhere but differentiable nowhere.