Angle between Two Lines

The angle formed by two lines It is useful to understand the relationship between the two lines. This will be the angle of inclination between two lines. There are two angles formed by two intersecting lines: the acute angle and the obtuse angle. Once two straight lines intersect, two sets of angles are formed. The intersection generates two acute angles and two obtuse angles. The absolute values of the formed angles are determined by the slopes of the intersecting lines. We regard the acute angle between two lines when calculating the angle between them. We could use the angle formed by two lines to calculate the angle formed by two sides of a closed polygon.

It’s also worth noting that the angle formed by the intersection of two lines cannot be calculated if one of the lines is parallel to the y-axis because the slope of a line parallel to the y-axis is indeterminate.

Angle Between Two Straight Lines Formula

If θ is an angle formed by two intersecting lines defined by y₁= m₁x₁+c₁ and y₂= m₂x₂+c_2,, the angle will be:

tanθ = ±(m₂-m₁) / (1+m₁m₂)

Angle Between Two Straight Lines Derivation

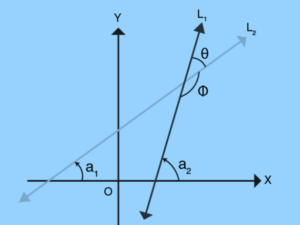
Lines L₁ and line L₂ intersect at a point in the figure above.

Now, the slope measurement is quite as follows:

tan a₁ = m₁ and tan a₂ = m₂

Then, from the figure, we can infer that θ = a₂-a₁

So, tan θ = tan (a₂-a₁) = (tan a₂ – tan a₁ ) / (1- tan a₁tan a₂)

When substituting the values of tan a₁ and tan a₂ as m₁ and m₂ respectively, we have,

tanθ= (m₂ – m₁) / (1+m₁m₂)

It must be observed that in this equation, the value of tanθ will be positive if θ is acute and negative if θ is obtuse.

Angle Between Two Lines Coordinate Geometry

If indeed the coordinates of three points A, B, and C are given in analytic geometry, the angle between the lines AB and BC can be calculated as follows:

The slope of a line with endpoints (x₁, y₁) and (x₂, y₂) is given by the equation:

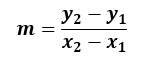
Whenever the slope of each line is known from the equation, the angle between the two lines can be calculated by calculating the slope of each line and then using it in the formula to determine the angle between two lines.

tan θ=± (m₁ – m₂) / (1+ m₁m₂)

FAQs

How to find the angle between the two lines with regards to a triangle?

First and foremost, the cosine rule must be applied. The values for the sides b, c, and angle A must then be entered. Following that, one must solve for side a. The angle value must then be used in conjunction with the sine rule to deal with angle B. At last, angle C can be found by remembering that the angles of all triangles add up to 180 degrees.

What is the angle between two perpendicular lines?

The angle formed by two perpendicular lines has always been 90°. This one is referred to as the right angle. The property of being perpendicular refers to the relationship that exists between two lines that meet at a right angle (90 degrees).