Arithmetico geometric series

Introduction

The term-by-term multiplication of a geometric sequence with the corresponding terms of just an arithmetic progression generates an arithmetic-geometric sequence in mathematics. Simply put, the nth term of an arithmetic-geometric series is the sum of the nth terms of the arithmetic and geometric sequences.

A brief outline

Arithmetic–geometric sequences can be found in a variety of contexts, including the computation of predicted values in probability theory. Counting the expected number of trials till success, for example.

Important concepts

Arithmetic-geometric progression is the mixture of arithmetic and geometric progression.

The nth term of A.G.P.

If a₁, a₂, a₃, ……. a_n, ……. = A.P and

b₁, b₂, b₃, ……. b_n, ……. = G.P,

then the sequence a₁b₁, a₂b₂, a₃b₃, ………, a_nb_n, ……. is said to be an arithmetico-geometric sequence.

Therefore, the overall form of an arithmetico geometric sequence is a, (a + d)r, (a + 2d)r², (a + 3d)r³, ………

The method for calculating the sum:

This approach may be used to calculate sums of n terms as well as sums of an unlimited number of terms. Assume that the sum of the series is S, then multiply it by the G.P.’s common ratio and subtract. We’ll end up with a G.P. whose total is simple to calculate.

A sequence is a collection of digits in which numbers can repeat themselves. The total of all the items of a sequence is called a series. Numbers in a sequence are arranged in a specific pattern, and although the numbers in a series are essentially generalized, there is still some relationship between them.

Sequence and series may appear to be extremely similar at first glance, but as you practice more problems, you will notice the differences. The number of elements in a sequence is represented by the term length. The main distinction is that numbers in a series have a probability of being repeated. Arithmetic sequences, geometric sequences, and other forms of sequences exist.

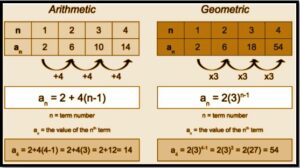
Significance of Arithmetic-geometric series in IIT JEE exam

The airthmetico geometric series is a crucial topic that necessitates a strong grasp of equations. Only equation-based questions will receive a response. On the IIT JEE exam, approximately 4 to 5 questions will be asked, accounting for 6.66 per cent of the total.

FAQs

Is it possible for arithmetic and geometric sequences to be the same?

Among arithmetic and geometric sequences, there are distinct differences as well as similarities. By adding, arithmetic sequences or series track terms. Multiplications follow terms in geometric series or sequences. The similarities between AP and GP are that they both follow a set of rules. This pattern is unbreakable.

What use does arithmetic progression serve?

The huge benefit of AP is that it may be used to forecast future statistics and trends. By evaluating the nth term in the AP sequence, we can rapidly obtain the following figures.

What method would you use to calculate the GP normal proportion?

To calculate a GP's typical proportion, divide the second term of the arrangement by the first term, or track down the proportion of any two consecutive terms by using the previous term as the denominator