Table of Contents
The motion of an object is claimed to be circular if it moves in an exceedingly way that distance from the centre point always remains identical. When any object is roughly moving on a circular path it’s called circular motion. The speed of the body during the motion can either change or even be identical throughout the entire motion. However, the rate and direction of the motion will change because its direction is changing at every point of the circle.
Examples of circular movements include artificial satellites orbiting the planet at a set height, wind turbines round the harp, a stone tied to a rope and thrown during a circle, a car that turns a race. track, an electron moving perpendicular to the identical field of force, and a rotating gear inside the machine.
Angular variables:
(1) Angular Displacement:
Defined because the angle is rotated by rotating particles during each unit. it’s represented by ∆θ and is measured in radians.
(2) Angular speed:
It’s defined because of the degree of change within the angular displacement of particles in a very circular motion. it’s described as
ω = limΔt→0(Δθ ⁄Δt) = dθ/ dt
Angular speed is measured in radius / s. additionally to angular speed and angular speed, the particle in circular motion also has linear speed and parallel line speed.
v = ds / dt
v = | ds / dt |; s particle transfer
The Relationship Between Line Speed (V) and Angular Speed (Ω)
In the type of a vector
v = ω x i
When r is the vector of the realm of the particles it’s measured in regard to the centre of the circle.
(Or)
v = rω
The acceleration of particles in circular motion has two components:
Tangential acceleration is: this could be a part of the acceleration within the direction of particle speed.
to = d|v| /dt
Radial acceleration ar: this is often the acceleration part directed at the centre of the circle. This component creates a change within the direction of the particle speed within the circular motion.
ar = v2 / r = rω2
(3) Angular Acceleration
It is defined because the degree of angular fluctuations of rotating particles. Measured with rad / s2
α = dω / dt
dω / dt = d2θ / dt2
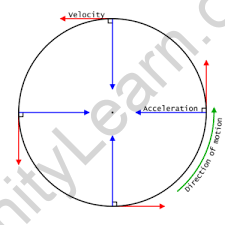
During a circular motion, the rate vector changes its direction at each point within the circle. this suggests that the radial acceleration portion remains zero. The tangential component can take a positive or negative value within the case of abnormal circular motion and a nil value within the case of the identical circular motion. We understand that the acceleration of particles in circular motion is usually centred and given v2 / r. Applying Newton’s second law of motion during this case; From = mv2 / r
When m is that the weight of the particles
Fc is that the central force-directed within the centre of a circular path as shown in
Types Of Circular Motion:
Uniform Circular Motion:
The movement of a body following a circular path is termed a circular motion. which means the motion of a body moving with constant speed in a circular path is called Uniform Circular Motion. Uniform circular motion tells the motion of an object traversing in a circular path at a constant speed. Since the body tells circular motion, the distance from the axis of rotation remains constant. Though the body’s speed is constant, its velocity isn’t constant: velocity, a vector quantity, depends on both the body’s speed and its direction of travel. This changing velocity represents the presence of acceleration, this centripetal acceleration is of the constant magnitude and directed in any respect times towards the axis of rotation. This acceleration is, in turn, produced by a force that is additionally constant in magnitude and directed towards the axis of rotation.
In the case of rotation around a fixed axis of a rigid body that’s not negligibly small compared to the radius of the trail, each particle of the body describes a regular circular motion with the identical angular velocity, but with velocity and acceleration varying with the position with reference to the axis.
In polar directions:
During roundabout movement, the body continues on a bend that may be depicted within the polar direction framework as an honest distance R from the focus of the circle taken as the beginning, focused at a degree θ(t) from some reference bearing. The dislodging vector is the outspread vector from the start to the molecule area: is the unit vector similar to the sweep vector at time t and pointing far from the start. it’s helpful to acquaint yourself with the unit vector symmetrical too, to be specific it’s standard to situate to point toward movement along the circle.
Non-Uniform Circular Motion:
Non-uniform circular motion is defined as a circular motion when the speed of the body doesn’t remain constant. The body has both normal still as tangential acceleration.
With an abnormal circular motion, normal force doesn’t always indicate the alternative of weight. Here is an example of something that goes straight and turns the loopback in the right direction again.
Examples of circular motions include a synthetic satellite orbiting the planet at a continuing height, wind turbines round the harp, a stone tied to a rope and a circular throw, a car turning a race. track, an electron moving perpendicular to the identical field of force, and a rotating gear inside the machine.
Side changes that occur are calculated by the radial acceleration given by the given number. i = v2r
FAQs
What's the circular motion called?
The motion is named uniform circular motion when the particle is moving along a circular path possessing a relentless speed. During circular motion, the rate vector changes its direction at each point on the circle.
Is circular motion easy for JEE?
It's a relatively simpler chapter. you'll be able to expect at the most one question from this chapter in JEE. This chapter forms a basis for the subsequent chapter called rotation, which is kind of important for JEE. So I might suggest you do not skip this chapter.









