Complex Numbers And Quadratic Equations Previous Year Questions With Solutions

Complex Numbers And Quadratic Equations

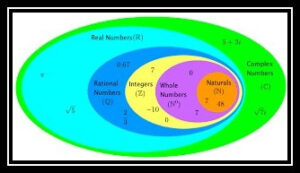
Complex numbers are characterized as quantities of the structure x+iy, where x and y are genuine numbers and I = √-1. For instance, 6+2i, – 6+i√3 are complicated numbers. For a complicated number z = x+iy, x is the genuine part, meant by Re z and y is known as the fanciful part signified by Im z. For instance, if z = 6+2i, Re z = 6 and Im z = 2.

In this segment, applicants will learn about complex numbers – definition, standard structure, mathematical activities, form, complex numbers’ polar structure, Euler’s structure and more. A Complex Number is a blend of a Real Number and an Imaginary Number.

What are Complex Numbers?

On the off chance that x, y ∈ R, an arranged pair (x, y) = x + iy is known as an intricate number. It is signified by z. Where x is a genuine piece of Re(z) and y is the nonexistent part or Im (z) of the perplexing number.

(I) If Re(z) = x = 0, then, at that point, it is called a nonexistent number

(ii) If Im(z) = y = 0 then z is called absolutely genuine number.

Note: The arrangement of all conceivable arranged sets, called complex number sets, is signified by C.

Quadratic Equations

Quadratic conditions are the polynomial conditions of degree 2 out of one variable of type f(x) = ax^2 + bx + c where a, b, c, ∈ R and a ≠ 0. It is the overall type of a quadratic condition where ‘a’ is known as the main coefficient, and ‘c’ is known as the outright f (x) term. The upsides of x fulfilling the quadratic condition are the foundations of the quadratic condition (α,β).

The quadratic condition will constantly have two roots. The idea of roots might be either genuine or nonexistent.

When compared to nothing, a quadratic polynomial turns into a quadratic condition. The upsides of x fulfilling the state are the foundations of the quadratic condition.

General from: ax^2 + bx + c = 0

Models: 3x^2 + x + 5 = 0, – x^2 + 7x + 5 = 0, x^2 + x = 0.

Quadratic Equation Formula

The quadratic equation gives the arrangement or underlying foundations of a quadratic condition:

(α, β) = [-b ± √(b^2 – 4ac)]/2ac

Previous Year Questions

Question 1: If (1 + i) (1 + 2i) (1 + 3i) ….. (1 + ni) = a + ib, then what is 2 * 5 * 10….(1 + n²) is equal to?

Solution:

Given (1 + i) (1 + 2i) (1 + 3i) ….. (1 + ni) = a + ib …..(i)

Assume, (1 − i) (1 − 2i) (1 − 3i) ….. (1 − ni) = a − ib …..(ii)

Multiplying (i) and (ii),

(1 + i)(1 – i) (1 + 2i)(1 – 2i) (1 + 3i)(1 – 3i) ….. (1 + ni)(1 – ni) = (a + ib)(a – bi)………..[(a + b)(a – b)= a² – b² ]

we get 2 * 5 * 10 ….. (1 + n²) = a² + b²

 

Question 2: If z is a complex number, then the minimum value of |z| + |z − 1| is ______.

Solution:

We know that, |−z|=|z| and |z₁ + z₂| ≤ |z₁| + |z₂|

So, |z| + |z − 1| = |z| + |1 − z| ≥ |z + (1 − z)|

= |1|

= 1

Therefore, the minimum value of |z| + |z − 1| is 1.

Question 3: Suppose z₁, z₂, and z₃ are the vertices of an equilateral triangle inscribed in the circle |z| = 2. If z₁ = 1 + i√3, find the values of z₃ and z₂.

Solution:

Given, z₁, z₂, and z₃ are the vertices of an equilateral triangle inscribed in the circle |z| = 2

So, from the above condition, we can assume that any one number must be conjugate of z₁ = 1 + i√3

i.e. z₂ = 1 − i√3 or z₃ = z₁ e^i2π/3 and

z₂ = z₁ e^−i2π/3 , z₃ = (1 + i√3) [cos (2π / 3) + i sin (2π / 3)] = −2

Therefore, the values of z₃ and z2 are z₂ = 1 − i√3 or z₃ = z₁ e^i2π/3 and z₂ = z₁ e^−i2π/3 , z₃ = (1 + i√3)

Question 4: If cosα + cos β + cos γ = sin α + sin β + sin γ = 0, then what is the value of cos 3α + cos 3β + cos 3γ?

Solution:

Given cos α + cos β + cos γ = 0 and sin α + sin β + sin γ = 0

Let us consider

a = cos α + i sin α;

b = cos β + i sin β and

c = cos γ + i sin γ.

Therefore, a + b + c = (cosα + cosβ + cosγ) + i (sinα + sinβ + sinγ) = 0 + i0 = 0

So, a + b + c = 0, then a³ + b³ + c³ = 3abc or

(cosα + isina)³ + (cosβ + isinβ)³ + (cosγ + isinγ)³ = 3 (cosα + isinα) (cosβ + isinβ) (cosγ + isinγ)

⇒ (cos3α + isin3α) + (cos3β + isin3β) + (cos3γ + isin3γ)

= 3 [cos (α + β + γ) + i sin (α + β + γ)] or cos 3α + cos 3β + cos 3γ

= 3 cos (α + β + γ).

The value of cos 3α + cos 3β + cos 3γ is 3 cos (α + β + γ)

Question 5: If the cube roots of unity are 1, ω, ω², then find the roots of the equation (x − 1)³ + 8 = 0.

Solution:

Given cube roots of unity are 1, ω, ω²

(x − 1)³ + 8 = 0

(x − 1)³ = −8

⇒ x − 1 = (−8)^1/3

x − 1 = −2, −2ω, −2ω²

x = −1, 1 − 2ω, 1 − 2ω²

The roots of the equation (x − 1)³ + 8 = 0 are x = −1, 1 − 2ω, 1 − 2ω²

Question 6: If 1, ω, ω², ω³……., ωⁿ⁻¹ are the n, n^th roots of unity, then (1 − ω) (1 − ω²) …..

(1 − ω^{n − 1}) = ____________.

Solution:

Given 1, ω, ω², ω³……., ωⁿ⁻¹ are the n, n^th roots of unity,

We can now consider,

= (x − 1) (x − ω) (x − ω²) ….. (x − ωⁿ⁻¹) = xⁿ − 1 or

(x − ω) (x − ω²)…..(x − ωⁿ⁻¹) = xⁿ−1 / x−1

= xⁿ⁻¹ + xⁿ⁻² +….. + x + 1

Substituting x = 1 on both sides, we get

(1 − ω) (1 − ω²)….. (1 − ωⁿ⁻¹) = n

The value of (1 − ω) (1 − ω²) ….. (1 − ω^{n − 1}) = n

Question 7: If a = cos (2π / 7) + i sin (2π / 7), then the quadratic equation whose roots are α = a + a² + a⁴ and β = a³ + a⁵ + a⁶ is _____________.

Solution:

Given a = cos (2π / 7) + i sin (2π / 7)

Now, a⁷ = [cos (2π / 7) + i sin (2π / 7)]⁷

= cos 2π + i sin 2π = 1 …..(i)

Given roots: α = a + a² + a⁴ and β = a³ + a⁵ + a⁶

So, the sum of the roots is

S = α + β = (a + a² + a⁴) + (a³ + a⁵ + a⁶)

S = a + a² + a³ + a⁴ + a⁵ + a⁶

=

$\frac{a(1-a^6)}{1-a}$

or S =

$\frac{a-1}{1-a}$

= −1 …..(ii)

The product of the roots is

P = α * β = (a + a² + a⁴) (a³ + a⁵ + a⁶)

= a⁴ + a⁶ + a⁷ + a⁵ + a⁷ + a⁸ + a⁷ + a⁹ + a¹⁰

= a⁴ + a⁶ + 1 + a⁵ + 1 + a + 1 + a² + a³ (From Eqn (i)]

= 3+(a + a² + a³ + a⁴ + a⁵ + a⁶)

= 3 + S = 3 − 1 = 2 [From (ii)]

So, the equation is, x² − Sx + P = 0

x² + x + 2 = 0.

The quadratic equation whose roots are α = a + a² + a⁴ and β = a³ + a⁵ + a⁶ is x² + x + 2 = 0

Question 8: (cos θ + i sin θ)⁴ / (sin θ + i cos θ)⁵ is equal to ____________.

Solution:

Given (cos θ + i sin θ)⁴ / (sin θ + i cos θ)⁵

= (cos θ + i sin θ)⁴ / i⁵ ([1 / i] sin θ + cos θ)⁵

= (cosθ + i sin θ)⁴ / i (cos θ − i sin θ)⁵

= (cos θ + i sin θ)⁴ / i (cos θ + i sin θ)⁻⁵ (By property)

= 1 / i (cos θ + i sin θ)⁹

= sin(9θ) − i cos (9θ).

(cos θ + i sin θ)⁴ / (sin θ + i cos θ)⁵ is equal to sin(9θ) − i cos (9θ)

 

FAQ’S

What are the Applications of Complex Numbers?

The idea of the perplexing number is utilized in various logical fields, which incorporate liquid elements, quantum mechanics, vibration investigation, signal handling, map making, electromagnetism, control hypothesis, and more. These, however, the idea of intricate numbers additionally shape the structure square of different points in your higher investigations.

Define Complex Numbers.

A complex number is characterized as a number that can be communicated as a + ib. Here, an and b are genuine numbers, and I am a particle. The worth of the particle is √-1. Along these lines, z (complex number) = a + ib where an is the genuine part, and ib is the nonexistent part. a = Re (z), b= Im (z).

Does the quadratic recipe work for complex numbers?

We can tackle quadratic conditions with complex coefficients utilizing the quadratic equation. On the off chance that the discriminant is zero, the condition has one rehashed root. Assuming every one of the coefficients is genuine, the root will be genuine.