Table of Contents
Many distinguishing properties of conic sections in the Euclidean plane can be used as alternative definitions. A non-circular conic is defined as the set of points whose distances to a specific point, called a focus, and a specific line, called a directrix, are in a fixed ratio, called the eccentricity. The value of the eccentricity determines the type of conic. A conic is defined in analytic geometry as a plane algebraic curve of degree 2; that is, the set of points whose coordinates satisfy a quadratic equation in two variables that can be written in matrix form. This equation allows you to deduce and express the geometric properties of conic sections algebraically.
One of the most important topics in Geometry is conic sections. In mathematics, there are various types of conic sections that can be defined based on the angle formed between the plane and the intersection of the right circular cone with it. A ‘conic’ curve is one that is formed by intersecting a right circular cone with a plane.
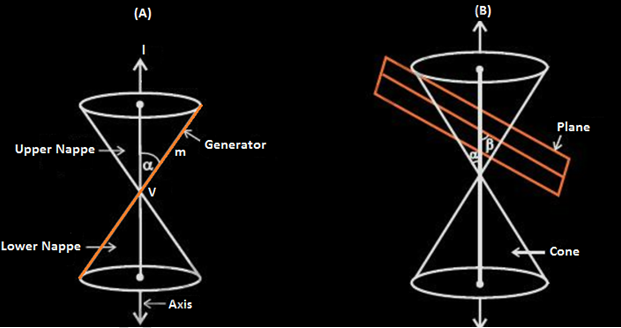
It has notable properties in Euclidean geometry. The cone is divided into two nappes by its vertex, which is referred to as the upper nappe and the lower nappe.
Conic Section Formulas
| Circle | (x−a)2+(y−b)2=r2 | Center is (a,b) Radius is r |
| Ellipse with the horizontal major axis | x−a)2/h2+(y−b)2/k2=1 | Center is (a, b) The length of the major axis is 2h. The length of the minor axis is 2k. Distance between the centre and either focus is c with c2=h2−k2, h>k>0 |
| Ellipse with the vertical major axis | (x−a)2/k2+(y−b)2/h2=1 | Center is (a, b) The length of the major axis is 2h. The length of the minor axis is 2k. Distance between the centre and either focus is c with c2=h2−k2, h>k>0 |
| Hyperbola with the horizontal transverse axis | (x−a)2/h2−(y−b)2/k2=1 | Center is (a,b) Distance between the vertices is 2h The distance between the foci is 2k. c2=h2 + k2 |
| Hyperbola with the vertical transverse axis | (x−a)2/k2−(y−b)2/h2=1 | Center is (a,b) Distance between the vertices is 2h The distance between the foci is 2k. c2= h2 + k2 |
Also read: How To Find The Area Of A Triangle Using Vectors?
Focus, Eccentricity, and Directrix of Conic
A conic section is also defined as the locus of a point P moving in the plane of a fixed point F known as focus (F) and a fixed line d known as directrix (with the focus not on d) such that the ratio of point P’s distance from focus F to its distance from d is a constant e known as eccentricity.
Now,
If the eccentricity, e, is zero, the conic is a circle.
If it is 01, it is a hyperbola.
So eccentricity is a measure of the ellipse’s deviation from being circular. Assume that the angle formed between the cone’s surface and its axis is and that the angle formed between the cutting plane and the axis is e = cos α/cos β
Also read: How To Find Slope Of Normal To Curve?
FAQs
In real life, what is a conic section?
Conic sections can be seen in a variety of real-world situations. For example, if we consider the Sun as a single point of focus, the paths of the planets form ellipses around it. Parabolic mirrors aid in the collection of light beams at the parabola's focus.
What is the significance of conic sections in mathematics?
Conic section analysis is important not only for mathematics, physics, and astronomy but also for a wide range of engineering applications. Conic section smoothness is an important property for applications such as aerodynamics, where a smooth surface is required to ensure laminar flow and avoid turbulence.



