Table of Contents
Observing the free oscillations of a real physical system, on the other hand, reveals that the oscillator’s energy gradually decreases with time, and the oscillator eventually comes to rest. For example, the amplitude of an oscillating pendulum in the air decreases over time and eventually stops. With the passage of time, the vibrations of a tuning fork fade away. This occurs because friction (or damping) is always present in physical systems. Friction is the resistance to motion. The presence of resistance to motion implies that the system is subjected to a frictional or damping force. The damping force acts in opposition to the motion, doing negative work on the system and causing energy to be dissipated. When a body moves through a medium such as air, water, or ice, its energy is dissipated due to friction and appears as heat in the body, the surrounding medium, or both. Another mechanism by which an oscillator loses energy exists. An oscillator’s energy can be reduced not only by friction in the system but also by radiation. The oscillating body causes periodic motion in the particles of the medium in which it oscillates, resulting in waves.
A tuning fork, for example, generates sound waves in the medium, causing its energy to decrease. All sounding bodies are subject to dissipative forces; otherwise, the body would lose no energy and therefore emit no sound energy. As a result of the radiation of mechanical oscillatory systems, sound waves are produced. We will discover later that electromagnetic waves are created by radiations from oscillating electric and magnetic fields.
The amplitude of oscillations gradually decreases with time as a result of radiation by an oscillating system and friction in the system. The reduction in amplitude (or energy) of an oscillator is referred to as damping, and the oscillation is referred to as being damped.
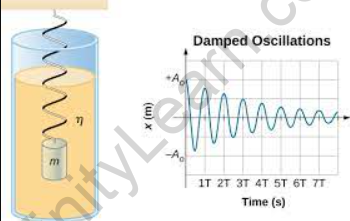
Damped oscillation
An oscillator is defined as anything with a rhythmic periodic response. A damped oscillation is one that gradually fades away with time. A swinging pendulum, a weight on a spring, and a resistor-inductor-capacitor (RLC) circuit are all examples. Assume we have an RLC circuit with a resistor, inductor, and capacitor in series. The capacitor will discharge into a series resistor and inductor when the switch is closed at time t=0. Now, the voltages and currents in this circuit can be calculated using
and V = starting voltage
C stands for capacitance (farads)
R stands for resistance (ohms)
L stands for inductance (henrys)
e = natural log base (2.71828…)
The current for a damped sine wave is given by the equation above. It is a maximum amplitude sine wave (V/BL) multiplied by an exponential decay damping factor. The time variation that results is an oscillation bounded by a decaying envelope.
Damping at Critical Points
These equations can be used to determine whether the energy fades out smoothly (over-damped) or rings out (under-damped).
FAQs
What exactly is damped oscillation?
Damped oscillation refers to an oscillation that fades over time. The amplitude of the oscillation decreases over time due to damping. The system's amplitude is reduced as a result of energy lost in overcoming external forces such as friction, air resistance, and other resistive forces.
Damped harmonic oscillation is a term used to describe a type of oscillation that has been dampened
Damped harmonic oscillators are vibrating systems whose amplitude decreases over time.






