Table of Contents
Differential Equations
A differential equation is a mathematical equation that contains one or more functions and their derivatives. The function’s derivatives describe the rate of change of a function at a given point. This is primarily used in fields such as physics, engineering, and biology. The main objective of differential equations is to investigate the solutions that satisfy the equations as well as the properties of the solutions. Applying explicit formulas is one of the simplest ways to solve the differential equation.
| S.NO | CONTENT |
| 1 | INTRODUCTION |
| 2 | ORDER OF DIFFERENTIAL EQUATION |
| 3 | DEGREE OF DIFFERENTIAL EQUATION |
| 4 | TYPES OF DIFFERENTIAL EQUATION |
| 5 | DIFFERENTIAL EQUATION SOLUTIONS |
| 6 | APPLICATION |
| 7 | FAQ’S |
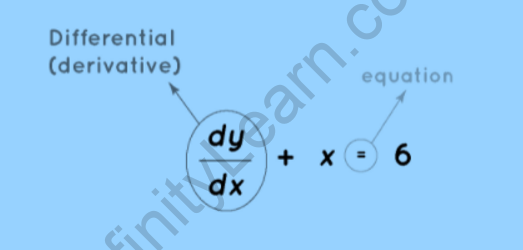
A differential equation is an equation that includes one or more terms as well as the derivatives of one variable (the dependent variable) with respect to another variable (i.e., independent variable)
dy/dx = f(x)
In which, “x” is considered as an independent variable, while “y” is a dependent variable.
A differential equation represents derivatives, which can be either partial or ordinary. The derivative denotes a rate of change, and the differential equation describes a relationship between one quantity that is constantly changing and another quantity that is changing. There really are numerous differential equation formulas for determining derivative solutions.
Order of Differential Equation
The order of a differential equation is indeed the order of the equation’s highest order derivative.
First Order Differential Equation: Each and every linear equation in the form of derivatives are of the first order. It only has the first derivative, such as dy/dx, where x and y are the two variables, and is denoted as:
dy/dx = f(x, y) = y’
Second-Order Differential Equation: The second-order differential equation is really the equation that includes the second-order derivative. It must be written as follows:
d/dx(dy/dx) = d2y/dx2 = f”(x) = y”
Degree of Differential Equation
The degree of the differential equation seems to be the power of the highest order derivative, in which the original equation is represented in derivatives such as y’,y”, y”‘, and so on.
A differential equation’s order and degree (if defined) have always been positive integers.
Types of Differential Equations
- Ordinary Differential Equations
- Partial Differential Equations
- Linear Differential Equations
- Nonlinear differential equations
- Homogeneous Differential Equations
- Nonhomogeneous Differential Equations
Differential Equations Solutions
A function that solves the given differential equation is referred to as its solution. A general solution would be one that contains as many arbitrary constants as the order of the differential equation. A particular solution is something that is free of arbitrary constants. There really are two approaches to solving the differential equation.
(1) Separation of variables
(2) Integrating factor
Applications
- Differential equations are being used to describe the growth and decay of various exponential functions.
- They are often used to describe how the return on investment changes over time.
- They have been used in medical science to simulate cancer growth or disease spread in the body.
- This can also be used to describe the movement of electricity.
- They aid economists in developing optimal investment strategies.
- Such equations can also be used to describe the motion of waves or a pendulum.
FAQs
What is the order of the differential Equation?
The order of the differential equation has been defined as the order of the highest order derivative present in the differential equation. The differential equation is seen as being of the first order if its order is one. If indeed the order of the equation is 2, it is referred to as a second-order equation, and so on.
What is the use of a differential equation?
The differential equation’s primary function is just to compute the function over its entire domain. It’s a term that describes the exponential growth or decay of a system over time. It’s indeed capable of predicting the world around us. This is commonly used in the field, including physics, chemistry, biology, and economics.
for more visit Solve Separable Differential Equations – Variable Separable Method









