Table of Contents
Besides integration, differentiation has been one of the two most important concepts in calculus. Differentiation is just a technique for determining a function’s derivative. Differentiation is really a mathematical process that determines the instantaneous rate of change of a function based on one of its variables. One of most typical example is velocity, which is the rate of change of displacement with respect to time. Anti-differentiation seems to be the inverse of finding a derivative.
If x is just a variable and y is yet another variable, then dy/dx represents the rate of change of x with respect to y. That’s the general expression for a function’s derivative and is represented as f'(x) = dy/dx, where y = f(x) can be any function.
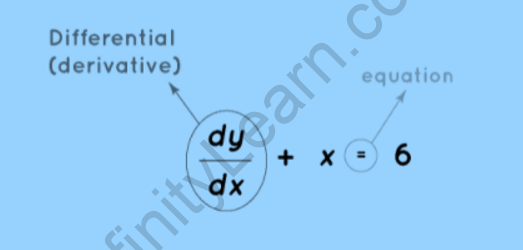
Differentiation has been defined in mathematics as the derivative of a function with respect to an independent variable. In advanced math, differentiation can be used to calculate the function per unit change in the independent variable.
Assume that y = f(x) is a function of x. Afterwards, for each unit change in “x,” the rate of change of “y” is given by:
dy / dx
If indeed the function f(x) undergoes an infinitesimal change of ‘h’ near any point ‘x’, the function’s derivative has been defined as:
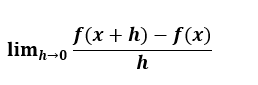
Derivative of Function as Limits
When we have a real-valued function (f) and x is a point in its domain of definition, the derivative of a function, f, has always been given by:
f'(a) = limit→0[f(x+h)-f(x)]/h
Notations
Whenever a function is denoted as y=f(x), the derivative is denoted by the notations shown below:
- D(y) or D[f(x)]: Euler’s notation.
- dy/dx: Leibniz’s notation.
- F’(x): Lagrange’s notation.
The method of determining the derivative of a function at any point has been defined as differentiation.
Linear and Non-Linear Functions
A linear function does have a constant rate of variation across its domain. As a result, the function’s overall rate of change is the same as the rate of change of a function at any point.
Even so, in the case of non-linear functions, the rate of change of the function varies from point to point. The aspect of variation would be determined by the function.
A derivative of a function has been defined as the rate of change of that function at a specific point.
Real-Life Applications of Differentiation
We could perhaps calculate the rate of change of one quantity in relation to another using differentiation. Here are a few examples:
- Acceleration is said to be the rate at which velocity changes with respect to time.
- The derivative function calculates the highest and lowest points of a curve in a graph or determines its turning point.
- For determining the tangent and normal to a curve
FAQs
What are the examples of differentiation?
Velocity is really an example of differentiation because it is equal to the rate of change of displacement with respect to time. Some other example is acceleration, which would be defined as the rate at which velocity changes with respect to time.
What is the derivative of sine function?
Once we differentiate sin x with respect to x, we get cos x as the derivative.







