Dimensions of Area: The area of a two-dimensional region, shape, or planar lamina in the plane is the quantity that expresses its extent. Surface area is indeed the two-dimensional surface of a three-dimensional object’s analogue. The area could be defined as the amount of material of a given thickness required to fashion a model of the shape or the amount of paint required to cover the surface in a single coat. It’s really the two-dimensional equivalent of a curve’s length (a one-dimensional concept) or a solid’s volume (a three-dimensional concept).
The area of a shape can always be calculated by comparing it to squares of a specific size and the standard unit of area in the International System of Units (SI) is the square metre (written as m2), which is the area of a square with one-metre-long sides. A three-square-metre-area shape would have the same area as three such squares. The area of the unit square is one in mathematics, and the area of any other shape or surface is a dimensionless real number.
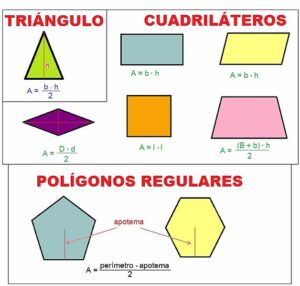
For the areas of simple shapes like triangles, rectangles, and circles, there are several well-known formulas. The area of any polygon could be calculated using these formulas by dividing the polygon into triangles. Calculus has been usually required to compute the area of shapes with curved boundaries. The method of finding the area of plane figures was, in fact, a major motivator for the historical development of calculus.
In modern mathematics, the area is very important. The area is related to the definition of determinants in linear algebra and is a basic property of surfaces in differential geometry, in addition to its obvious importance in geometry and calculus. The area of a subset of the plane is defined in analysis using the Lebesgue measure, though not every subset is measurable. In higher mathematics, the area is viewed as a special case of volume for two-dimensional regions.
Axioms could be used to define the area as a function of a collection of certain plane figures to the set of real numbers. It’s indeed possible to show that such a function exists.
Dimensional Formula of Area
The dimensional formula of the area can be represented as:
[M0 L2 T0]
Here,
M = Mass
L = Length
T = Time
Derivation:
We have, Area (A) = Length × breadth . . . . (1)
Then, the dimensional formula of length = [M0 L1 T0] . . . . (2)
Now, when substituting equation (2) in equation (1) we get,
Area = Length × breadth
That is, A = [M0 L1 T0] × [M0 L1 T0] = [M0 L2 T0]
Thus, area has been dimensionally represented as [M0 L2 T0].
Also Read: Dimensions Of Electric Flux | Dimensions Of Work | Dimensions Of Light Year
FAQs
. ” image-1=”” count=”2″ html=”true” css_class=””]


