Table of Contents
Dimensions of the physical quantity are the strength to which the base portions are raised to symbolize that amount. Dimensions of any given quantity tell us approximately how and in which way extraordinary bodily quantities are related. Finding dimensions of different physical quantities has many real-life programs and is helpful in locating gadgets and measurements. Imagine a physical amount X which depends especially on base mass(m), duration(L), and time(T) with their respective powers, and then we can constitute the dimensional formula as [MaLbTc].
Dimensional Formula
The dimensional formulation of any physical quantity is that expression that represents how and which of the base portions are blanketed in that quantity.
It is written by enclosing the symbols for base quantities with appropriate power in rectangular brackets i.E ( ).E.G: Dimension formulation of mass is: (M)
Dimensional Equation
The equation obtained by way of equating a physical quantity with its dimensional formula is known as a dimensional equation.
Application of Dimensional Analysis
To convert a bodily amount from one device of the unit to the other:
It is based totally on a truth that the magnitude of a physical quantity stays identical anything gadget is used for size i.E magnitude = numeric value(n) elevated with the aid of unit (u) = constant
n1u1= n1u2
To take a look at the dimensional correctness of a given bodily relation:
If in a given relation, the terms of each side have identical dimensions, then the equation is dimensionally correct. This idea is first-class, known as the precept of homogeneity of dimensions.
To derive a courting between exclusive bodily portions:
Using the principle of homogeneity of measurement, the brand new relation among physical portions can be derived if the dependent quantities are regarded.
Limitation of this Method
This method can be used simplest if dependency is of multiplication kind. The components containing exponential, trigonometric, and logarithmic capabilities can not be derived using this technique. The formulation containing multiple terms which are delivered or subtracted likes s = ut+ ½ at2 also cannot be derived.
The relation derived from this technique offers no records about the dimensionless constants.
Electric Current
When rate flows in a conductor from one vicinity to every other, then the fee of drift of price is referred to as electric contemporary. When there is a switch of price from one point to every other point in a conductor, we are saying that there’s electric current via the place. If the moving charge is wonderful, the contemporary is in the path of the fee. If transferring costs are negative the modern is opposite to the route of movement of charge.
If a rate ∂Q crosses an area in time ∂t, we define average electric powered current via the area, during this time as
Average cutting-edge I(common) = ∂Q∂t
Instantaneous modern = dQdt
Unit of contemporary is ampere (A) or coulomb/sec
i.E Q= ne therefore I=ne/t
Here n= quantity of loose electrons
t= time wherein n electron passes via it
e= charge on electron
Properties of Electric Current
The go with the flow of electrons through a conductor is known as strength, and an electric modern-day tends to generate warmness power.
An electric modern-day is the drift of rate in line with unit time.
There is a relation between the amount of cutting-edge and the voltage that pushes the electrons at the side of the diploma of resistance to waft.
The SI unit of electrical modern is ampere. It is denoted via ‘A’.
The longer the cutting-edge flow via a conductor, the extra the heat is generated.
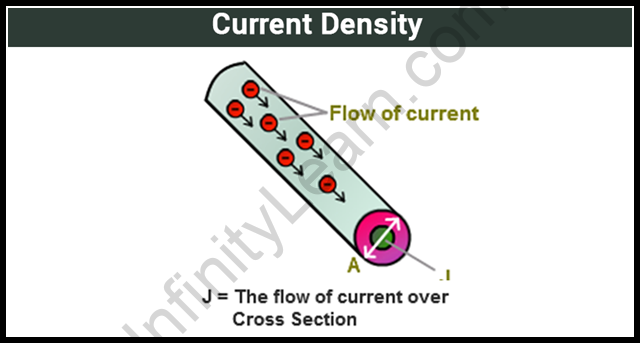
Current Density
The present-day density at a point in a conductor is the ratio of the modern at that point inside the conductor to the place of move segment of the conductor of that factor.
Unit = amperemetre
J=dIdA
, here dA is the move-section region
Application of Current Density
Current density plays a critical position in the outward spectrum that is produced in gas discharge lamps, like flash lamps.
High modern-day densities
These are much more likely to favour shorter wavelengths and are more at risk of producing continuum emissions.
Low cutting-edge densities
These, alternatively, are more likely to favour longer wavelengths and are more vulnerable to generating spectral line emissions.
The Dimension of Current Density
The dimensional formula of modern density is given by using M0 L-2 T0 I1
Where well-known unit mass is represented as M, modern-day via I, duration by way of L, and time through T.
Increase and Decrease of Current Density
The contemporary density can be higher in a conductor if the modern in it’s far excessive. But the cutting-edge density tends to adjust in specific parts of an electric conductor. And the impact tends to take place with alternating currents at better frequencies.
When the charging current increases, the time this is required to build up the equal fee/voltage tends to lower proportionally. Therefore, the charging-discharging time cycle tends to decrease proportional to the current, while the modern will increase.
Derivation of the Dimensional Formula of Current Density
Formula of Current Density = Charge ×(Area × Time1) . . . (1)
As fee = contemporary × time
Therefore, the scale of electrical charge may be written as M0L0I1T1 . . . . (2)
And, the dimensional formulation of some required devices are given beneath:
Area = [M0 L2 T0] . . . (3)
Time = [M0 L0 T1] . . . . (4)
On placing equation (2) and (3) in equation (1) we get,
Current Density = Charge × Area×Time-1
= [M0 L0 I1 T1] × [M0 L2 T0]-1 × [M0 L0 T1]-1 = [M0 L-2 T0 I1].
Therefore, the dimensional formulation of modern density is represented as [M0 L-2 T0 I1].
FAQs:
Q. Define Dimension Formula.
Ans: Dimensions of the physical quantity are the power to which the base quantities are raised to represent that quantity. The dimensional formula of any physical quantity is that expression that represents how and which of the base quantities are included in that quantity.
It is written by enclosing the symbols for base quantities with appropriate power in square brackets i.e. ( ).
Q. Explain a Few Limitations of Dimension Formulas.
Ans: Some of the limitations of the dimension formula are given below:
- This method can be used only if dependency is of multiplication type. The formula containing exponential, trigonometric and logarithmic functions can not be derived using this method. A formula containing more than one term which is added or subtracted likes s = ut+ ½ at² also cannot be derived.
- The relation derived from this method gives no information about the dimensionless constants.








