Table of Contents
The quantity of any characteristic value per unit length is known as linear density. Two common examples used in science and engineering are linear mass density (titer in textile engineering, the amount of mass per unit length) and linear charge density (the amount of electric charge per unit length).
The term linear density is most commonly used to describe the properties of one-dimensional objects, but it can also be used to describe the density of a three-dimensional quantity along one dimension.
Just as density is frequently used to refer to mass density, linear density is frequently used to refer to linear mass density. However, this is only one example of a linear density because any quantity can be measured in terms of its value along a single dimension.
Many methods exist for measuring the linear density of fibres and yarns.
The most basic is to measure and weigh the length of the material. This, however, necessitates a large sample size, masks the variability of linear density along the thread, and is difficult to apply if the fibres are crimped or otherwise cannot lay flat relaxed.
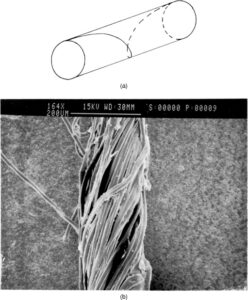
If the density of the material is known, the fibres are measured individually and have a simple shape; however, direct imaging of the fibre with SEM to measure the diameter and calculate the linear density is a more accurate method. Finally, linear density is measured directly with a vibroscope. The sample is tensioned between two hardpoints, mechanical vibration is produced, and the fundamental frequency is determined.
The ability to perform an activity is defined as energy. Work, on the other hand, is defined as a force acting over a distance, so the basic dimensional units of energy are force x distance. Depending on the unit of measurement, this could be dyne-centimetres, Newton-metres, or foot-pounds. Any combination of force and distance could be used to measure energy. A few of these units have unique names. A Newton-metre is also known as a Joule. Joules are most commonly found on surge suppressors. An erg is defined as a dyne-centimetre (a unit of energy that is equivalent to 10 joules). There is also Ergometer exercise equipment.
Dimensional Formula of Linear Density
Linear Density’s dimensional formula is given by,
M1 L-1 T0
Where M stands for mass.
T = Time L = Length
Linear Density (ρ) = Mass × [Length]-1 . . . (1)
The mass dimensional formula = [M1 L0 T0] . . . . (2)
The length dimensional formula = [M0 L1 T0] . . . . (3)
When we substitute equations (2) and (3) into equation (1), we get
Linear Density = Mass × [Length]-1
Or, ρ = [M1 L0 T0] × [M0 L1 T0]-1 = [M1 L-1 T0].
As a result, the linear density is represented dimensionally as [M1 L-1 T0].
FAQs
What does the linear density of charge mean?
Linear charge density () is the amount of charge per unit length at any point on a line charge distribution, measured in coulombs per metre (Cm1). Because electric charge can be either positive or negative, charge density can be either positive or negative.
What is the linear density law?
If the tension and vibrating length of a string are constant, the fundamental frequency of its vibrations is inversely proportional to the square root of its mass per unit length (linear density).





